Article contents
Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux
Published online by Cambridge University Press: 11 November 2013
Abstract
We employ direct numerical simulation to investigate the efficiency of diapycnal mixing by shear-induced turbulence in stably stratified free shear layers for flows with bulk Richardson numbers in the range 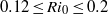 $0. 12\leq R{i}_{0} \leq 0. 2$ and Reynolds number
$0. 12\leq R{i}_{0} \leq 0. 2$ and Reynolds number 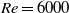 $Re= 6000$ . We show that mixing efficiency depends non-monotonically upon
$Re= 6000$ . We show that mixing efficiency depends non-monotonically upon 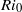 $R{i}_{0} $ , peaking in the range 0.14–0.16, which coincides closely with the range in which both the buoyancy flux and the dissipation rate are maximum. By detailed analyses of the energetics of flow evolution and the underlying dynamics, we show that the existence of high mixing efficiency in the range
$R{i}_{0} $ , peaking in the range 0.14–0.16, which coincides closely with the range in which both the buoyancy flux and the dissipation rate are maximum. By detailed analyses of the energetics of flow evolution and the underlying dynamics, we show that the existence of high mixing efficiency in the range 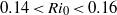 $0. 14\lt R{i}_{0} \lt 0. 16$ is due to the emergence of a large number of small-scale instabilities which do not exist at lower Richardson numbers and are stabilized at high Richardson numbers. As discussed in Mashayek & Peltier (J. Fluid Mech., vol. 725, 2013, pp. 216–261), the existence of such a well-populated ‘zoo’ of secondary instabilities at intermediate Richardson numbers and the subsequent high mixing efficiency is realized only if the Reynolds number is higher than a critical value which is generally higher than that achievable in laboratory settings, as well as that which was achieved in the majority of previous numerical studies of shear-induced stratified turbulence. We furthermore show that the primary assumptions upon which the widely employed Osborn (J. Phys. Oceanogr. vol. 10, 1980, pp. 83–89) formula is based, as well as its counterparts and derivatives, which relate buoyancy flux to dissipation rate through a (constant) flux coefficient (
$0. 14\lt R{i}_{0} \lt 0. 16$ is due to the emergence of a large number of small-scale instabilities which do not exist at lower Richardson numbers and are stabilized at high Richardson numbers. As discussed in Mashayek & Peltier (J. Fluid Mech., vol. 725, 2013, pp. 216–261), the existence of such a well-populated ‘zoo’ of secondary instabilities at intermediate Richardson numbers and the subsequent high mixing efficiency is realized only if the Reynolds number is higher than a critical value which is generally higher than that achievable in laboratory settings, as well as that which was achieved in the majority of previous numerical studies of shear-induced stratified turbulence. We furthermore show that the primary assumptions upon which the widely employed Osborn (J. Phys. Oceanogr. vol. 10, 1980, pp. 83–89) formula is based, as well as its counterparts and derivatives, which relate buoyancy flux to dissipation rate through a (constant) flux coefficient ( 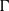 $\Gamma $ ), fail at higher Richardson numbers provided that the Reynolds number is sufficiently high. Specifically, we show that the assumptions of fully developed, stationary, and isotropic turbulence all break down at high Richardson numbers. We show that the breakdown of these assumptions occurs most prominently at Richardson numbers above that corresponding to the maximum mixing efficiency, a fact that highlights the importance of the non-monotonicity of the dependence of mixing efficiency upon Richardson number, which we establish to be characteristic of stratified shear-induced turbulence. At high
$\Gamma $ ), fail at higher Richardson numbers provided that the Reynolds number is sufficiently high. Specifically, we show that the assumptions of fully developed, stationary, and isotropic turbulence all break down at high Richardson numbers. We show that the breakdown of these assumptions occurs most prominently at Richardson numbers above that corresponding to the maximum mixing efficiency, a fact that highlights the importance of the non-monotonicity of the dependence of mixing efficiency upon Richardson number, which we establish to be characteristic of stratified shear-induced turbulence. At high 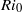 $R{i}_{0} $ , the lifecycle of the turbulence is composed of a rapidly growing phase followed by a phase of rapid decay. Throughout the lifecycle, there is considerable exchange of energy between the small-scale turbulence and larger coherent structures which survive the various stages of flow evolution. Since shear instability is one of the most prominent mechanisms for turbulent dissipation of energy at scales below hundreds of metres and at various depths of the ocean, our results have important implications for the inference of turbulent diffusivities on the basis of microstructure measurements in the oceanic environment.
$R{i}_{0} $ , the lifecycle of the turbulence is composed of a rapidly growing phase followed by a phase of rapid decay. Throughout the lifecycle, there is considerable exchange of energy between the small-scale turbulence and larger coherent structures which survive the various stages of flow evolution. Since shear instability is one of the most prominent mechanisms for turbulent dissipation of energy at scales below hundreds of metres and at various depths of the ocean, our results have important implications for the inference of turbulent diffusivities on the basis of microstructure measurements in the oceanic environment.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
Mashayek et al. supplementary movie
The XZ view of the rate of dissipation of kinetic energy for Ri=0.14. Open this file side by side movie 2.
Mashayek et al. supplementary movie
The YZ view of the rate of dissipation of kinetic energy for Ri=0.14. Open this file side by side movie 1.
- 68
- Cited by

