Hostname: page-component-76c49bb84f-lxspr Total loading time: 0 Render date: 2025-07-12T16:13:54.060Z Has data issue: false hasContentIssue false
  • English
  • Français

Tilting of vortex rings in the oblique collision reduces the longitudinal quadrupole and octupole modes of aerodynamic sound

Published online by Cambridge University Press:  11 July 2025

Zhenyu Zang ,
Zhiteng Zhou ,
Yi Liu  and
Shizhao Wang Open the ORCID record for Shizhao Wang [Opens in a new window]
Zhenyu Zang
Affiliation:
The State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, PR China
Zhiteng Zhou
Affiliation:
The State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, PR China
Yi Liu
Affiliation:
The State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, PR China
Shizhao Wang*
Affiliation:
The State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, PR China
*
Corresponding author: Shizhao Wang, wangsz@lnm.imech.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

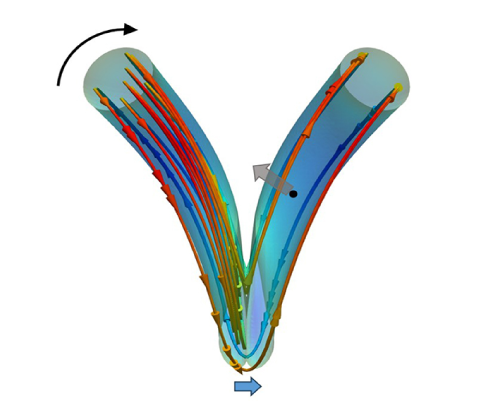
The aerodynamic sound generated by the oblique collision of two vortex rings is featured by the asymmetric emission associated with the octupole mode, which differs from the symmetric emission associated with the quadrupole mode observed in the coaxial collision of two vortex rings. This distinctive feature of aerodynamic sound is closely related to the tilting and reconnecting of the vortex rings. While previous studies have explored the effects of reconnecting on aerodynamic sound, this study specifically addresses the impact of vortex ring tilting. We propose a novel vortex sound formula to quantitatively assess the role of tilting in aerodynamic sound generation. The proposed formula relates the far-field sound pressure to equivalent circulations and vorticity centroids by referring to Truesdell’s consistency conditions for vorticity moments. The variations of the equivalent circulations and vorticity centroids in the oblique collision of two vortex rings under different configurations are analysed based on the numerical solution of the Navier–Stokes equations in the source region. It is found that the tilting of vortex rings results in a rapid change of the equivalent circulation associated with the vorticity in the collision direction. However, the change caused by titling is almost out of phase with that caused by reconnecting and deforming. The vortex tilting significantly reduces the aerodynamic sound associated with the longitudinal quadrupole and octupole modes, which is opposite to the role of vortex reconnecting that was reported in the oblique collision of vortex rings.

JFM classification

Acoustics: Aeroacoustics Vortex Flows: Vortex dynamics

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1015 , 25 July 2025 , A1
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahmed, T. & Erath, B.D. 2023 Experimental study of vortex ring impingement on concave hemispherical cavities. J. Fluid Mech. 967, A38.10.1017/jfm.2023.501CrossRefGoogle Scholar
Batchelor, G.K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.10.1017/CBO9780511800955CrossRefGoogle Scholar
Borisov, A.V., Kilin, A.A. & Mamaev, I.S. 2013 The dynamics of vortex rings: Leapfrogging, choreographies and the stability problem. Regular Chaotic Dyn. 18 (1-2), 33–62.10.1134/S1560354713010036CrossRefGoogle Scholar
Chen, H., Yoas, Z.W., Jaworski, J.W. & Krane, M.H. 2022 Acoustic emission of a vortex ring near a porous edge. Part 1: theory. J. Fluid Mech. 941, 941 A28-1–941 A28-17.10.1017/jfm.2022.313CrossRefGoogle Scholar
Chu, C.-C., Wang, C.-T., Chang, C.-C., Chang, R.-Y. & Chang, W.-T. 1995 Head-on collision of two coaxial vortex rings: experiment and computation. J. Fluid Mech. 296, 39–71.10.1017/S0022112095002060CrossRefGoogle Scholar
Daryan, H., Hussain, F. & Hickey, J.-P. 2020 Aeroacoustic noise generation due to vortex reconnection. Phys. Rev. Fluids 5 (6), 062702.10.1103/PhysRevFluids.5.062702CrossRefGoogle Scholar
Daryan, H., Hussain, F. & Hickey, J.-P. 2022 Sound generation mechanism of compressible vortex reconnection. J. Fluid Mech. 933, A34.10.1017/jfm.2021.1088CrossRefGoogle Scholar
Dyson, F.W. & Thomson, J.J. 1893 XX. The potential of an anchor ring.-Part II. Phil. Trans. R. Soc. Lond. (A.) 184, 1041–1106.Google Scholar
Eldredge, J.D. 2007 The dynamics and acoustics of viscous two-dimensional leapfrogging vortices. J. Sound Vib. 301 (1-2), 74–92.10.1016/j.jsv.2006.09.015CrossRefGoogle Scholar
Falahatpisheh, A. & Kheradvar, A. 2015 A measure of axisymmetry for vortex rings. Eur. J. Mech.-B/Fluids 49, 264–271.10.1016/j.euromechflu.2014.09.003CrossRefGoogle Scholar
Feng, F., Meng, X., Guo, L. & Wang, Q. 2020 Directivity of acoustic field generated by leapfrogging. 32 (12), 126106.Google Scholar
Hattori, Y., Blanco-Rodríguez, F.J. & Le Dizès, S. 2019 Numerical stability analysis of a vortex ring with swirl. J. Fluid Mech. 878, 5–36.10.1017/jfm.2019.621CrossRefGoogle Scholar
He, G., Jin, G. & Yang, Y. 2017 Space-time correlations and dynamic coupling in turbulent flows. Annu. Rev. Fluid Mech. 49 (1), 51–70.10.1146/annurev-fluid-010816-060309CrossRefGoogle Scholar
Hernandez, R.H. & Reyes, T. 2017 Symmetrical collision of multiple vortex rings. Phys. Fluids 29 (10), 103604.10.1063/1.5004587CrossRefGoogle Scholar
Hu, J. & Peterson, S.D. 2021 The influence of collision angle for viscous vortex reconnection. Phys. Fluids 33 (9), 093608.10.1063/5.0064720CrossRefGoogle Scholar
Hussain, A.K.M.F. & Zaman, K.B.M.Q. 1981 The preferred mode of the axisymmetric jet. J. Fluid Mech. 110 (SEP), 39–71.10.1017/S0022112081000608CrossRefGoogle Scholar
Hussain, F. & Duraisamy, K. 2011 Mechanics of viscous vortex reconnection. Phys. Fluids 23 (2), 021701.10.1063/1.3532039CrossRefGoogle Scholar
Inoue, O. 2002 Sound generation by the leapfrogging between two coaxial vortex rings. Phys. Fluids 14 (9), 3361–3364.10.1063/1.1500360CrossRefGoogle Scholar
Inoue, O., Hattori, Y. & Sasaki, T. 2000 Sound generation by coaxial collision of two vortex rings. J. Fluid Mech. 424, 327–365.10.1017/S0022112000002123CrossRefGoogle Scholar
Ishii, K., Kuwahara, K. & Liu, C.H. 1993 Navier–Stokes calculations for vortex rings in an unbounded domain. Comput. Fluids 22 (4-5), 589–605.10.1016/0045-7930(93)90027-7CrossRefGoogle Scholar
Kambe, T. 2010 Vortex sound with special reference to vortex rings: theory, computer simulations, and experiments. Intl J. Aeroacoust. 9 (1-2), 51–89.10.1260/1475-472X.9.1-2.51CrossRefGoogle Scholar
Kambe, T. & Minota, T. 1981 Sound radiation from vortex systems. J. Sound Vib. 74 (1), 61–72.10.1016/0022-460X(81)90491-0CrossRefGoogle Scholar
Kambe, T. & Minota, T. 1983 Acoustic wave radiated by head-on collision of two vortex rings. Proc. R. Soc. Lond. A. Math. Phys. Sci. 386 (1791), 277–308.Google Scholar
Kambe, T., Minota, T. & Takaoka, M. 1993 Oblique collision of two vortex rings and its acoustic emission. Phys. Rev. E 48 (3), 1866–1881.10.1103/PhysRevE.48.1866CrossRefGoogle ScholarPubMed
Kida, S., Takaoka, M. & Hussain, F. 1991 Collision of two vortex rings. J. Fluid Mech. 230, 583–646.10.1017/S0022112091000903CrossRefGoogle Scholar
Limbourg, R. & Nedić, J. 2021 An extension to the universal time scale for vortex ring formation. J. Fluid Mech. 915, A46.10.1017/jfm.2021.141CrossRefGoogle Scholar
Liu, Y., Wang, H., Wang, S. & He, G. 2023 A cache-efficient reordering method for unstructured meshes with applications to wall-resolved large-eddy simulations. J. Comput. Phys. 480, 112009.10.1016/j.jcp.2023.112009CrossRefGoogle Scholar
Matsuzawa, T., Mitchell, N.P., Perrard, S. & Irvine, W.T.M. 2023 Creation of an isolated turbulent blob fed by vortex rings. Nat. Phys. 19 (8), 1–8.10.1038/s41567-023-02052-0CrossRefGoogle Scholar
McKeown, R., Ostilla-Mónico, R., Pumir, A., Brenner, M.P. & Rubinstein, S.M. 2018 Emergence of small scales in vortex ring collisions. Phys. Rev. Fluids 3 (10), 100509.10.1103/PhysRevFluids.3.100509CrossRefGoogle Scholar
Meleshko, V.V. 2010 Coaxial axisymmetric vortex rings: 150 years after Helmholtz. Theor. Comput. Fluid Dyn. 24 (1-4), 403–431.10.1007/s00162-009-0148-zCrossRefGoogle Scholar
Mishra, A., Pumir, A. & Ostilla-Mónico, R. 2021 Instability and disintegration of vortex rings during head-on collisions and wall interactions. Phys. Rev. Fluids 6 (10), 104702.10.1103/PhysRevFluids.6.104702CrossRefGoogle Scholar
Möhring, W. 1978 On vortex sound at low Mach number. J. Fluid Mech. 85 (4), 685–691.10.1017/S0022112078000865CrossRefGoogle Scholar
Nakashima, Y. 2008 Sound generation by head-on and oblique collisions of two vortex rings. Phys. Fluids 20 (5), 056102.10.1063/1.2919521CrossRefGoogle Scholar
New, T.H., Long, J., Zang, B. & Shi, S. 2020 Collision of vortex rings upon V-walls. J. Fluid Mech. 899, A2.10.1017/jfm.2020.425CrossRefGoogle Scholar
Nguyen, V.L. 2022 Turbulent energy cascade and mixing induced by the axis-offset collision of two vortex rings. Fluid Dyn. 57 (6), 845–864.10.1134/S0015462822100391CrossRefGoogle Scholar
Ortega-Chavez, R., Gan, L. & Gaskell, P.H. 2023 Formation and evolution of vortex rings with weak to moderate swirl. J. Fluid Mech. 967, A16.10.1017/jfm.2023.482CrossRefGoogle Scholar
Saffman, P.G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49 (4), 371–380.10.1002/sapm1970494371CrossRefGoogle Scholar
Saffman, P.G. 1995 Vortex Dynamics. Cambridge University Press.Google Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24 (1), 235–279.10.1146/annurev.fl.24.010192.001315CrossRefGoogle Scholar
Shen, W., Yao, J., Hussain, F. & Yang, Y. 2023 Role of internal structures within a vortex in helicity dynamics. J. Fluid Mech. 970, A26.10.1017/jfm.2023.620CrossRefGoogle Scholar
Stumpf, M.P.H. & Porter, M.A. 2012 Critical truths about power laws. Science 335 (6069), 665–666.10.1126/science.1216142CrossRefGoogle ScholarPubMed
Tang, S.K. & Ko, N.W.M. 1995 a Sound generation by a vortex ring collision. J. Acoust. Soc. Am. 98 (6), 3418–3427.10.1121/1.413793CrossRefGoogle Scholar
Tang, S.K. & Ko, N.W.M. 2000 Sound sources in the interactions of two inviscid two-dimensional vortex pairs. J. Fluid Mech. 419, 177–201.10.1017/S0022112000001294CrossRefGoogle Scholar
Tang, S.K. & Ko, N.W.M. 1995 b On sound generated from the interaction of two inviscid coaxial vortex rings moving in the same direction. J. Sound Vib. 187 (2), 287–310.10.1006/jsvi.1995.0522CrossRefGoogle Scholar
Truesdell, C. 2018 The Kinematics of Vorticity. Courier Dover Publications.Google Scholar
Verzicco, R., Iafrati, A., Riccardi, G. & Fatica, M. 1997 Analysis of the sound generated by the pairing of two axisymmetric co-rotating vortex rings. J. Sound Vib. 200 (3), 347–358.10.1006/jsvi.1996.0714CrossRefGoogle Scholar
Wang, L. & Feng, L.-H. 2022 Dynamics of the interaction of synthetic jet vortex rings with a stratified interface. J. Fluid Mech. 943, A1.10.1017/jfm.2022.379CrossRefGoogle Scholar
Weller, H.G., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12 (6), 620–631.10.1063/1.168744CrossRefGoogle Scholar
Yao, J. & Hussain, F. 2020 A physical model of turbulence cascade via vortex reconnection sequence and avalanche. J. Fluid Mech. 883, A51.10.1017/jfm.2019.905CrossRefGoogle Scholar
Yao, J. & Hussain, F. 2022 Vortex reconnection and turbulence cascade. Annu. Rev. Fluid Mech. 54 (1), 317–347.10.1146/annurev-fluid-030121-125143CrossRefGoogle Scholar