Article contents
Three-dimensional wave packet in a Mach 6 boundary layer on a flared cone
Published online by Cambridge University Press: 27 December 2019
Abstract
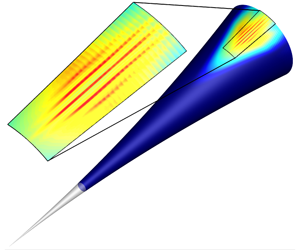
High-resolution direct numerical simulations (DNS) were carried out to investigate the nonlinear breakdown process of a three-dimensional wave packet initiated by a short-duration pulse in a flared cone boundary layer at Mach 6 and zero angle of attack. For these simulations the cone geometry of the flared cone experiments conducted in the Boeing/AFOSR Mach 6 Quiet Tunnel (BAM6QT) at Purdue University was considered. The computational domain covered a large extent of the cone in the azimuthal direction to allow for a wide range of azimuthal wavenumbers ( $k_{c}$) and to include shallow instability waves with small azimuthal wavenumbers. The simulation results indicated that the wave packet development was dominated by axisymmetric and shallow (small
$k_{c}$) and to include shallow instability waves with small azimuthal wavenumbers. The simulation results indicated that the wave packet development was dominated by axisymmetric and shallow (small  $k_{c}$) second-mode waves for a large downstream extent. Towards the downstream end of the computational domain a rapid broadening of the disturbance amplitude spectra was observed, which is an indication that the wave packet reached the strongly nonlinear stages. The disturbance spectra of the nonlinear regime, and the downstream amplitude development of the dominant disturbance wave components, provided conclusive evidence that the so-called fundamental breakdown was the dominant nonlinear mechanism. Furthermore, contours of the time-averaged Stanton number exhibited ‘hot’ streaks within the wave packet on the surface of the cone. Hot streaks have also been observed in the Purdue flared cone experiments using temperature sensitive paint (TSP) and in numerical investigations using DNS. The azimuthal streak spacing obtained from the wave packet simulation agrees well with that observed in the Purdue quiet tunnel experiments.
$k_{c}$) second-mode waves for a large downstream extent. Towards the downstream end of the computational domain a rapid broadening of the disturbance amplitude spectra was observed, which is an indication that the wave packet reached the strongly nonlinear stages. The disturbance spectra of the nonlinear regime, and the downstream amplitude development of the dominant disturbance wave components, provided conclusive evidence that the so-called fundamental breakdown was the dominant nonlinear mechanism. Furthermore, contours of the time-averaged Stanton number exhibited ‘hot’ streaks within the wave packet on the surface of the cone. Hot streaks have also been observed in the Purdue flared cone experiments using temperature sensitive paint (TSP) and in numerical investigations using DNS. The azimuthal streak spacing obtained from the wave packet simulation agrees well with that observed in the Purdue quiet tunnel experiments.
Information
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2019. Published by Cambridge University Press
References
- 41
- Cited by

