Article contents
Three-dimensional quasi-geostrophic vortex equilibria with 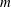 $m$-fold symmetry
$m$-fold symmetry
Published online by Cambridge University Press: 22 January 2019
Abstract
We investigate arrays of 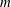 $m$ three-dimensional, unit-Burger-number, quasi-geostrophic vortices in mutual equilibrium whose centroids lie on a horizontal circular ring; or
$m$ three-dimensional, unit-Burger-number, quasi-geostrophic vortices in mutual equilibrium whose centroids lie on a horizontal circular ring; or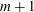 $m+1$ vortices where the additional vortex lies on the vertical ‘central’ axis passing through the centre of the array. We first analyse the linear stability of circular point vortex arrays. Three distinct categories of vortex arrays are considered. In the first category, the
$m+1$ vortices where the additional vortex lies on the vertical ‘central’ axis passing through the centre of the array. We first analyse the linear stability of circular point vortex arrays. Three distinct categories of vortex arrays are considered. In the first category, the 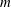 $m$ identical point vortices are equally spaced on a circular ring and no vortex is located on the vertical central axis. In the other two categories, a ‘central’ vortex is added. The latter two categories differ by the sign of the central vortex. We next turn our attention to finite-volume vortices for the same three categories. The vortices consist of finite volumes of uniform potential vorticity, and the equilibrium vortex arrays have an (imposed)
$m$ identical point vortices are equally spaced on a circular ring and no vortex is located on the vertical central axis. In the other two categories, a ‘central’ vortex is added. The latter two categories differ by the sign of the central vortex. We next turn our attention to finite-volume vortices for the same three categories. The vortices consist of finite volumes of uniform potential vorticity, and the equilibrium vortex arrays have an (imposed) 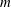 $m$-fold symmetry. For simplicity, all vortices have the same volume and the same potential vorticity, in absolute value. For such finite-volume vortex arrays, we determine families of equilibria which are spanned by the ratio of a distance separating the vortices and the array centre to the vortices’ mean radius. We determine numerically the shape of the equilibria for
$m$-fold symmetry. For simplicity, all vortices have the same volume and the same potential vorticity, in absolute value. For such finite-volume vortex arrays, we determine families of equilibria which are spanned by the ratio of a distance separating the vortices and the array centre to the vortices’ mean radius. We determine numerically the shape of the equilibria for 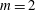 $m=2$ up to
$m=2$ up to 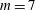 $m=7$, for each three categories, and we address their linear stability. For the
$m=7$, for each three categories, and we address their linear stability. For the  $m$-vortex circular arrays, all configurations with
$m$-vortex circular arrays, all configurations with 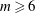 $m\geqslant 6$ are unstable. Point vortex arrays are linearly stable for
$m\geqslant 6$ are unstable. Point vortex arrays are linearly stable for 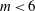 $m<6$. Finite-volume vortices may, however, be sensitive to instabilities deforming the vortices for
$m<6$. Finite-volume vortices may, however, be sensitive to instabilities deforming the vortices for 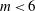 $m<6$ if the ratio of the distance separating the vortices to their mean radius is smaller than a threshold depending on
$m<6$ if the ratio of the distance separating the vortices to their mean radius is smaller than a threshold depending on 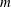 $m$. Adding a vortex on the central axis modifies the overall stability properties of the vortex arrays. For
$m$. Adding a vortex on the central axis modifies the overall stability properties of the vortex arrays. For 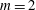 $m=2$, a central vortex tends to destabilise the vortex array unless the central vortex has opposite sign and is intense. For
$m=2$, a central vortex tends to destabilise the vortex array unless the central vortex has opposite sign and is intense. For 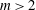 $m>2$, the unstable regime can be obtained if the strength of the central vortex is larger in magnitude than a threshold depending on the number of vortices. This is true whether the central vortex has the same sign as or the opposite sign to the peripheral vortices. A moderate-strength like-signed central vortex tends, however, to stabilise the vortex array when located near the plane containing the array. On the contrary, most of the vortex arrays with an opposite-signed central vortex are unstable.
$m>2$, the unstable regime can be obtained if the strength of the central vortex is larger in magnitude than a threshold depending on the number of vortices. This is true whether the central vortex has the same sign as or the opposite sign to the peripheral vortices. A moderate-strength like-signed central vortex tends, however, to stabilise the vortex array when located near the plane containing the array. On the contrary, most of the vortex arrays with an opposite-signed central vortex are unstable.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 23
- Cited by
Linked content
Please note that this article has a (1).

