Article contents
Three-dimensional organization and dynamics of vortices in multichannel swirling jets
Published online by Cambridge University Press: 21 March 2018
Abstract
The unsteady three-dimensional flow organization of jets issued from a duct with swirl vanes at Reynolds number equal to 1000 and swirl number 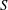 $S$ ranging between 0 and 0.8 is investigated. Time-resolved tomographic particle image velocimetry returns the instantaneous flow structure and its evolution by visualization of velocity and vortical features. The most relevant coherent motions are identified and characterized with the aid of dynamic mode decomposition. The time-averaged flow topology indicates that the vanes used to impart the swirling motion have a significant impact on the azimuthal modulation of momentum, with the jet exhibiting four sectors separated by a thin cross-like wake resulting from the boundary layer developed along the vane walls. The flow field is thus characterized by inner and outer shear regions. An increase in swirl, up to moderate levels (
$S$ ranging between 0 and 0.8 is investigated. Time-resolved tomographic particle image velocimetry returns the instantaneous flow structure and its evolution by visualization of velocity and vortical features. The most relevant coherent motions are identified and characterized with the aid of dynamic mode decomposition. The time-averaged flow topology indicates that the vanes used to impart the swirling motion have a significant impact on the azimuthal modulation of momentum, with the jet exhibiting four sectors separated by a thin cross-like wake resulting from the boundary layer developed along the vane walls. The flow field is thus characterized by inner and outer shear regions. An increase in swirl, up to moderate levels (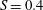 $S=0.4$), causes larger jet spreading angles. Further increase of the swirl number is accompanied by the appearance of a central recirculation zone due to vortex breakdown at
$S=0.4$), causes larger jet spreading angles. Further increase of the swirl number is accompanied by the appearance of a central recirculation zone due to vortex breakdown at  $S=0.6$ which increases in size and is triggered upstream for increasing
$S=0.6$ which increases in size and is triggered upstream for increasing 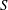 $S$. Although no shear layer instability development is observed at
$S$. Although no shear layer instability development is observed at 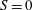 $S=0$, already at
$S=0$, already at 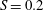 $S=0.2$ the swirling motion promotes the growth of helical vortices appearing as Kelvin–Helmholtz waves that deform the outer axial shear layer. The downstream evolution features successive pairing, which is observed for all the considered swirl numbers. The initial development of the instability is independent for each vane, whereas a mutual interaction between the vanes occurs after the vortex pairing. The reconnection from the four sectors vortices induces a significant increase of azimuthal vorticity, which affects the dynamical behaviour of the precessing vortex core. The latter is visualized by a low-order spatio-temporal reconstruction based on few dynamical modes. At a higher swirl number (
$S=0.2$ the swirling motion promotes the growth of helical vortices appearing as Kelvin–Helmholtz waves that deform the outer axial shear layer. The downstream evolution features successive pairing, which is observed for all the considered swirl numbers. The initial development of the instability is independent for each vane, whereas a mutual interaction between the vanes occurs after the vortex pairing. The reconnection from the four sectors vortices induces a significant increase of azimuthal vorticity, which affects the dynamical behaviour of the precessing vortex core. The latter is visualized by a low-order spatio-temporal reconstruction based on few dynamical modes. At a higher swirl number (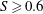 $S\geqslant 0.6$), the axial vorticity component dominates the flow field; it interacts with the azimuthal vorticity, which penetrates inward through the meanders of the vane wakes and forces the vortex core precession and breakdown.
$S\geqslant 0.6$), the axial vorticity component dominates the flow field; it interacts with the azimuthal vorticity, which penetrates inward through the meanders of the vane wakes and forces the vortex core precession and breakdown.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
Present address: Currently a postdoctoral appointee at Sandia National Laboratories, Albuquerque, NM, USA 87185.
Present address: Currently employed by the Innovation and Networks Executive Agency of the European Commission, Chaussée de Wavre 910, 1040 Etterbeek, Brussels, Belgium.
References
- 30
- Cited by

