Hostname: page-component-7dd5485656-gs9qr Total loading time: 0 Render date: 2025-10-31T20:10:37.617Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional effects on the transfer function of a rectangular-section body in turbulent flow

Published online by Cambridge University Press:  10 June 2019

Yang Yang Open the ORCID record for Yang Yang [Opens in a new window] ,
Mingshui Li  and
Haili Liao
Yang Yang
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China
Mingshui Li*
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China Key Laboratory for Wind Engineering of Sichuan Province, Chengdu 610031, China
Haili Liao
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China Key Laboratory for Wind Engineering of Sichuan Province, Chengdu 610031, China
*
†Email address for correspondence: lms_rcwe@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the influence of three-dimensional effects on the transfer function of a rectangular-section body in turbulent flow. The dimensionless factor 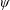$\unicode[STIX]{x1D713}$, as derived by Li et al. (J. Fluid Mech., vol. 847, 2018, pp. 768–785), is adapted to evaluate this influence. The calculation of 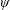$\unicode[STIX]{x1D713}$ requires the spanwise influence term. For this purpose, an adapted form of the lift coherence function is derived, enabling the use of the measured lift coherence for the estimation of the spanwise influence term. Three rectangular models with different cross-sections (chord-to-depth ratios of 3, 5 and 10) are chosen for testing, and a NACA 0015 airfoil model is tested for comparison. Using the measured spanwise influence terms, the dimensionless factors of these models are then numerically calculated under different ratios of the turbulent integral scale to the chord 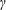$\unicode[STIX]{x1D6FE}$ and aspect ratios 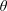$\unicode[STIX]{x1D703}$. It is shown that the dimensionless factors of the rectangular models increase as 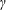$\unicode[STIX]{x1D6FE}$ and 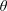$\unicode[STIX]{x1D703}$ increase, which are similar to the dimensionless factor of the airfoil model. If 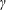$\unicode[STIX]{x1D6FE}$ and 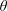$\unicode[STIX]{x1D703}$ have suitable values, the strip theory could be applicable to the rectangular-section body. It is also found that the dimensionless factors of all the rectangular models are larger than the dimensionless factor of the airfoil model under the same parameters. The smaller the chord-to-depth ratio is, the larger the dimensionless factor is. Using the strip theory to calculate the lift response of the rectangular-section body may provide more accurate estimation. Additionally, the one-wavenumber transfer functions of these models are determined under the consideration of the three-dimensional effects. The results show that the experimental transfer functions of the rectangular models cannot be captured by the Sears function. They are larger than the Sears function at lower frequencies, while falling at a faster rate as the frequency increases. For bluff bodies with separated flow, the modified transfer function presented here appears to be an appropriate approach.

JFM classification

Aerodynamics: Aerodynamics Turbulent Flows: Turbulent Flows

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 348 - 366
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Atassi, H. M. 1984 The Sears problem for a lifting airfoil revisited—new results. J. Fluid Mech. 141, 109–122.Google Scholar
Blake, W. K. 1986 Mechanics of Flow-Induced Sound and Vibration. Academic.Google Scholar
Etkin, B. 1959 A theory of the response of airplanes to random atmospheric turbulence. J. Aero. Sci. 26, 409–420.Google Scholar
Etkin, B. 1971 Dynamic of Atmospheric Flight. Wiley.Google Scholar
Goldstein, M. E. & Atassi, H. M. 1976 A complete second-order theory for the unsteady flow about an airfoil due to a periodic gust. J. Fluid Mech. 74, 741–765.Google Scholar
Graham, J. M. R. 1970 Lifting-surface theory for the problem of an arbitrary yawed sinusoidal gust incident on a thin aerofoil in incompressible flow. Aeronaut. Q. 21, 182–198.Google Scholar
Graham, J. M. R. 1971 A lift-surface theory for the rectangular wing in non-stationary flow. Aeronaut. Q. 22, 83–100.Google Scholar
Hakkinen, R. J. & Richardson, A. S.1957 Theoretical and experimental investigation of random gust loads. Part I. Aerodynamic transfer function of a simple wing configuration in incompressible flow. NACA Tech. Rep. 3878.Google Scholar
Jackson, R., Graham, J. M. R. & Maull, D. J. 1973 The lift on a wing in a turbulent flow. Aeronaut. Q. 24, 155–166.Google Scholar
Jakobsen, J. B. 1997 Span-wise structure of lift and overturning moment on a motionless bridge girder. J. Wind Engng Ind. Aerodyn. 69, 795–805.Google Scholar
Kimura, K., Fujino, Y., Nakato, S. & Tamura, H. 1997 Characteristics of buffeting forces on flat cylinders. J. Wind Engng Ind. Aerodyn. 69, 365–374.Google Scholar
Larose, G. L. 1999 Experimental determination of the aerodynamic admittance of a bridge deck segment. J. Fluid Struct. 13, 1029–1040.Google Scholar
Larose, G. L. & Mann, J. 1998 Gust loading on streamlined bridge decks. J. Fluid Struct. 12, 511–536.Google Scholar
Li, M., Yang, Y., Li, M. & Liao, H. 2018 Direct measurement of the Sears function in turbulent flow. J. Fluid Mech. 847, 768–785.Google Scholar
Li, S. & Li, M. 2017 Spectral analysis and coherence of aerodynamic lift on rectangular cylinders in turbulent flow. J. Fluid Mech. 830, 408–438.Google Scholar
Li, S., Li, M. & Liao, H. 2015 The lift on an aerofoil in grid-generated turbulence. J. Fluid Mech. 771, 16–35.Google Scholar
Liepmann, H. W. 1952 On the application of statistical concepts to buffeting problem. J. Aero. Sci. 19, 793–800.Google Scholar
Lysak, P. D., Capone, D. E. & Jonson, M. L. 2013 Prediction of high frequency gust response with airfoil thickness effects. J. Fluid Struct. 39, 258–274.Google Scholar
Ma, C.2007 3D Aerodynamic admittance research of streamlined box bridge decks. PhD thesis, Southwest Jiaotong University, Chengdu.Google Scholar
Massaro, M. & Graham, J. M. R. 2015 The effect of three-dimensionality on the aerodynamic admittance of thin sections in free stream turbulence. J. Fluid Struct. 57, 81–89.Google Scholar
McKeough, P.1976 Effects of turbulence on aerofoils at high incidence. PhD thesis, University of London.Google Scholar
Mugridge, B. D. 1971 Gust loading on a thin aerofoil. Aeronaut. Q. 22, 301–310.Google Scholar
Nagata, K., Hunt, J. C. R., Sakai, Y. & Wong, H. 2011 Distorted turbulence and secondary flow near right-angled plates. J. Fluid Mech. 668, 446–479.Google Scholar
Ribner, H. S. 1956 Spectral theory of buffeting and gust response: unification and extension. J. Aero. Sci. 23, 1075–1077.Google Scholar
Roberts, J. B. & Surry, D. 1973 Coherence of grid-generated turbulence. J. Engng Mech. Div. 99, 1227–1245.Google Scholar
Santana, L. D., Christophe, J., Schram, C. & Desmet, W. 2016 A rapid distortion theory modified turbulence spectra for semi-analytical airfoil noise prediction. J. Sound Vib. 383, 349–363.Google Scholar
Sears, R. W.1938 A systematic presentation of the theory of thin airfoils in non-uniform motion. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar