Article contents
Thermohaline staircase formation in the diffusive convection regime: a theory based upon stratified turbulence asymptotics
Published online by Cambridge University Press: 22 November 2021
Abstract
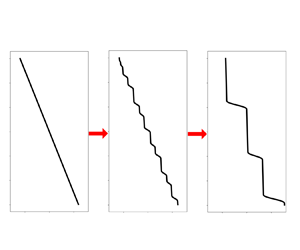
We describe a mechanism that leads to the spontaneous formation of a thermohaline staircase in the high-latitude oceans. Our analysis of this mechanism is based upon a model in which uniform gradients of temperature and salinity are assumed and is applied to a simplified mean-field model of stratified turbulence. Detailed analysis employs a parametrization of turbulent diapycnal diffusivities (Bouffard & Boegman, Dyn. Atmos. Oceans, vol. 61, 2013, pp. 14–34). This parametrization is apparently unique in that it distinguishes between the diapycnal diffusivities for heat and salt on the basis of their Prandtl (Schmidt) numbers. Our model predicts that the temperature and salinity profiles will be susceptible to linear instability if the buoyancy Reynolds number lies in the range 0.18–91, and a nonlinear mean-field model simulation demonstrates that it evolves into a well-defined thermohaline staircase that matches the characteristics of those found in the high-latitude oceans. The criterion for initial instability is furthermore shown to be consistent with the observed regional variability of staircase occurrence in the Arctic Ocean as determined by the most recent observational datasets.
Information
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 12
- Cited by


