Article contents
Test section streaks originating from imperfections in a zither located upstream of a contraction
Published online by Cambridge University Press: 15 December 2015
Abstract
Defining a link between wind-tunnel settling chamber screens, flow quality and test section boundary-layer spanwise variation is necessary for accurate transition prediction. The aim of this work is to begin establishing this link. The computed, steady, laminar wake of a zither (screen model) with imperfect wire spacing is tracked through a contraction and into a model test section. The contraction converts the zither wake into streamwise vorticity which then creates spanwise variation (streaks) in the test-section boundary layer. The magnitude of the spanwise variation is sensitive to the zither open-area ratio and imperfections, but the observed wavelength is relatively insensitive to the zither wire spacing. Increased spanwise variation is attributed to large wavelength variation of drag across the zither, and not the coalescence of jets phenomena. The linear stability of the streaks is predicted using the parabolized stability equations with the 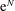 $\text{e}^{N}$ method. A standard deviation of zither wire position error of 38.1
$\text{e}^{N}$ method. A standard deviation of zither wire position error of 38.1 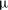 ${\rm\mu}$ m (15 % of wire diameter) for a zither of 50 % open-area ratio is found to suppress Tollmien–Schlichting wave growth significantly.
${\rm\mu}$ m (15 % of wire diameter) for a zither of 50 % open-area ratio is found to suppress Tollmien–Schlichting wave growth significantly.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 2
- Cited by


