Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Omidyeganeh, Mohammad
Piomelli, Ugo
Christensen, Kenneth T.
and
Best, James L.
2013.
Large eddy simulation of interacting barchan dunes in a steady, unidirectional flow.
Journal of Geophysical Research: Earth Surface,
Vol. 118,
Issue. 4,
p.
2089.
Franklin, Erick de Moraes
and
Ayek, Guilherme Augusto
2013.
The perturbation of a turbulent boundary layer by a two-dimensional hill.
Journal of the Brazilian Society of Mechanical Sciences and Engineering,
Vol. 35,
Issue. 4,
p.
337.
Makwana, Ajay B.
Patankar, Atharva
and
Bose, Manaswita
2015.
Effect of Dune Formation on Pressure Drop in Horizontal Pneumatic Conveying System.
Particulate Science and Technology,
Vol. 33,
Issue. 1,
p.
59.
Sotiropoulos, Fotis
and
Khosronejad, Ali
2016.
Sand waves in environmental flows: Insights gained by coupling large-eddy simulation with morphodynamics.
Physics of Fluids,
Vol. 28,
Issue. 2,
Bristow, N
Blois, G
Tang, Z
Barros, J
Best, J
and
Christensen, K
2016.
Measurements of flow dynamics associated with interacting, subaqueous barchans: Exploring bedform asymmetry and threedimensionality in a novel flume environment.
p.
443.
Jhalani, Sumit
Patankar, Atharva
Makawana, Ajay
Bose, Manaswita
Radjai, F.
Nezamabadi, S.
Luding, S.
and
Delenne, J.Y.
2017.
Dune formation in dilute phase pneumatic transport system: PIV & PTV based analysis.
EPJ Web of Conferences,
Vol. 140,
Issue. ,
p.
09007.
Atharva Patankar
Ajay Makawana
and
Manaswita Bose
2017.
Fluid Mechanics and Fluid Power – Contemporary Research.
p.
1609.
Khosronejad, A.
and
Sotiropoulos, F.
2017.
On the genesis and evolution of barchan dunes: morphodynamics.
Journal of Fluid Mechanics,
Vol. 815,
Issue. ,
p.
117.
Bristow, N. R.
Blois, G.
Best, J. L.
and
Christensen, K. T.
2018.
Turbulent Flow Structure Associated With Collision Between Laterally Offset, Fixed‐Bed Barchan Dunes.
Journal of Geophysical Research: Earth Surface,
Vol. 123,
Issue. 9,
p.
2157.
Cúñez, Fernando David
Gomes de Oliveira, Gabriel Victor
and
de Moraes Franklin, Erick
2018.
Turbulent channel flow perturbed by triangular ripples.
Journal of the Brazilian Society of Mechanical Sciences and Engineering,
Vol. 40,
Issue. 3,
Wenzel, João Luiz
and
de Moraes Franklin, Erick
2019.
Velocity fields and particle trajectories for bed load over subaqueous barchan dunes.
Granular Matter,
Vol. 21,
Issue. 3,
Bristow, N. R.
Blois, G.
Best, J. L.
and
Christensen, K. T.
2019.
Spatial Scales of Turbulent Flow Structures Associated With Interacting Barchan Dunes.
Journal of Geophysical Research: Earth Surface,
Vol. 124,
Issue. 5,
p.
1175.
Zheng, Yan
Dong, Lin
and
Rinoshika, Akira
2019.
Multi-scale wake structures around the dune.
Experimental Thermal and Fluid Science,
Vol. 104,
Issue. ,
p.
209.
Khosronejad, Ali
Kang, Seokkoo
Farhadzadeh, Ali
and
Sotiropoulos, Fotis
2020.
On the genesis and evolution of barchan dunes: Hydrodynamics.
Physics of Fluids,
Vol. 32,
Issue. 8,
Alvarez, Carlos A.
and
Franklin, Erick M.
2020.
Shape evolution of numerically obtained subaqueous barchan dunes.
Physical Review E,
Vol. 101,
Issue. 1,
Jin, Chuang
Coco, Giovanni
Tinoco, Rafael O.
Perron, J. Taylor
Myrow, Paul M.
Huppert, Kimberly L.
Friedrich, Heide
Goldstein, Evan B.
and
Gong, Zheng
2020.
Investigating the response of wave-generated ripples to changes in wave forcing.
Geomorphology,
Vol. 363,
Issue. ,
p.
107229.
Bristow, N. R.
Blois, G.
Best, J. L.
and
Christensen, K. T.
2020.
Secondary Flows and Vortex Structure Associated With Isolated and Interacting Barchan Dunes.
Journal of Geophysical Research: Earth Surface,
Vol. 125,
Issue. 2,
Salimi‐Tarazouj, Ali
Hsu, Tian‐Jian
Traykovski, Peter
Cheng, Zhen
and
Chauchat, Julien
2021.
A Numerical Study of Onshore Ripple Migration Using a Eulerian Two‐phase Model.
Journal of Geophysical Research: Oceans,
Vol. 126,
Issue. 2,
Alvarez, Carlos A.
Cúñez, Fernando David
and
Franklin, Erick M.
2021.
Growth of barchan dunes of bidispersed granular mixtures.
Physics of Fluids,
Vol. 33,
Issue. 5,
Kidanemariam, Aman G.
Scherer, Markus
and
Uhlmann, Markus
2022.
Open-channel flow over evolving subaqueous ripples.
Journal of Fluid Mechanics,
Vol. 937,
Issue. ,
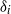 – is assessed. In the outer layer, streamline curvature is shown to be responsible for half of the Lagrangian speed-up, from the comparison of the velocity measurements with two Bernoulli calculations. In the inner layer, detailed measurements of the velocity and stresses are provided, down to
– is assessed. In the outer layer, streamline curvature is shown to be responsible for half of the Lagrangian speed-up, from the comparison of the velocity measurements with two Bernoulli calculations. In the inner layer, detailed measurements of the velocity and stresses are provided, down to 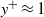 , and the momentum budget is discussed. The Reynolds shear stress decreases monotonically towards the dune surface, according to the standard mixing-length closure, whereas the total shear stress increases strongly in the viscous sublayer. Along the dune surface, the shear stress increases up to the crest where it reaches twice its unperturbed value. A good estimate of the surface stress is provided by a parabolic fit of the inner velocity profile matching the outer flow at
, and the momentum budget is discussed. The Reynolds shear stress decreases monotonically towards the dune surface, according to the standard mixing-length closure, whereas the total shear stress increases strongly in the viscous sublayer. Along the dune surface, the shear stress increases up to the crest where it reaches twice its unperturbed value. A good estimate of the surface stress is provided by a parabolic fit of the inner velocity profile matching the outer flow at 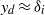 . Doubling the Reynolds number, the surface shear stress and the speed-up decrease by ∼30 %. The implications of these results on the dune motion, presented in Part 1 of this study (Franklin & Charru, J. Fluid Mech., vol. 675, 2011, pp. 199–222), are finally discussed.
. Doubling the Reynolds number, the surface shear stress and the speed-up decrease by ∼30 %. The implications of these results on the dune motion, presented in Part 1 of this study (Franklin & Charru, J. Fluid Mech., vol. 675, 2011, pp. 199–222), are finally discussed.