Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
Fan, Yitong
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012010.
Wu, Xiaohua
Moin, Parviz
and
Adrian, Ronald J.
2020.
Laminar to fully turbulent flow in a pipe: scalar patches, structural duality of turbulent spots and transitional overshoot.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Örlü, Ramis
and
Vinuesa, Ricardo
2020.
Instantaneous wall-shear-stress measurements: advances and application to near-wall extreme events.
Measurement Science and Technology,
Vol. 31,
Issue. 11,
p.
112001.
Chin, R. C.
Vinuesa, R.
Örlü, R.
Cardesa, J. I.
Noorani, A.
Chong, M. S.
and
Schlatter, P.
2020.
Backflow events under the effect of secondary flow of Prandtl's first kind.
Physical Review Fluids,
Vol. 5,
Issue. 7,
Guerrero, Byron
Lambert, Martin F.
and
Chin, Rey C.
2020.
Extreme wall shear stress events in turbulent pipe flows: spatial characteristics of coherent motions.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Chen, Tao
Liu, Tianshu
and
Wang, Lian-Ping
2021.
Features of surface physical quantities and temporal-spatial evolution of wall-normal enstrophy flux in wall-bounded flows.
Physics of Fluids,
Vol. 33,
Issue. 12,
Yang, Xiang I. A.
Hong, Jiarong
Lee, Myoungkyu
and
Huang, Xinyi L. D.
2021.
Grid resolution requirement for resolving rare and high intensity wall-shear stress events in direct numerical simulations.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Ivashchenko, V A
Zaripov, D I
and
Mullyadzhanov, R I
2021.
The effect of Reynolds number on near-wall reverse flow in a turbulent duct flow.
Journal of Physics: Conference Series,
Vol. 2119,
Issue. 1,
p.
012032.
Zaripov, Dinar
Ivashchenko, Vladislav
Mullyadzhanov, Rustam
Li, Renfu
Markovich, Dmitriy
and
Kähler, Christian J.
2021.
Reverse flow phenomenon in duct corners at a low Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 8,
Zaripov, Dinar
Ivashchenko, Vladislav
Mullyadzhanov, Rustam
Li, Renfu
Mikheev, Nikolay
and
Kähler, Christian J.
2021.
On a mechanism of near-wall reverse flow formation in a turbulent duct flow.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Zaripov, D I
2021.
Problems of an experimental study of a reverse flow in the turbulent channel flow.
Journal of Physics: Conference Series,
Vol. 2057,
Issue. 1,
p.
012097.
Tong, Fulin
Dong, Siwei
Duan, Junyi
Yuan, Xianxu
and
Li, Xinliang
2022.
Effect of expansion on the wall heat flux in a supersonic turbulent boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 10,
Guerrero, Byron
Lambert, Martin F.
and
Chin, Rey C.
2022.
Precursors of backflow events and their relationship with the near-wall self-sustaining process.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Dong, Siwei
Tong, Fulin
Yu, Ming
Chen, Jianqiang
Yuan, Xianxu
and
Wang, Qian
2022.
Positive and negative pairs of fluctuating wall shear stress and heat flux in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 8,
Tong, Fulin
Dong, Siwei
Lai, Jiang
Yuan, Xianxu
and
Li, Xinliang
2022.
Wall shear stress and wall heat flux in a supersonic turbulent boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 1,
Agrawal, Rishav
Mishra, Debi Prasad
and
Poole, Robert J.
2022.
Numerical study of wall shear stress fluctuations and near-wall structures in a square duct at low Reynolds numbers.
Computers & Fluids,
Vol. 249,
Issue. ,
p.
105688.
Zaripov, D. I.
Lukyanov, A. A.
and
Markovich, D. M.
2023.
Experimental investigation of instantaneous local flow separation in a turbulent boundary layer at various Reynolds numbers.
Thermophysics and Aeromechanics,
Vol. 29,
Issue. 5,
p.
647.
Chen, Tao
and
Liu, Tianshu
2023.
Lamb dilatation and its hydrodynamic viscous flux in near-wall incompressible flows.
Physica D: Nonlinear Phenomena,
Vol. 448,
Issue. ,
p.
133730.
Zaripov, Dinar
Li, Renfu
Lukyanov, Alexey
Skrypnik, Artem
Ivashchenko, Elizaveta
Mullyadzhanov, Rustam
and
Markovich, Dmitriy
2023.
Backflow phenomenon in converging and diverging channels.
Experiments in Fluids,
Vol. 64,
Issue. 1,
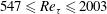 $547\leqslant Re_{\unicode[STIX]{x1D70F}}\leqslant 2003$. It is found that regions of backflow are attached and their density per surface area – in wall units – is an increasing function of
$547\leqslant Re_{\unicode[STIX]{x1D70F}}\leqslant 2003$. It is found that regions of backflow are attached and their density per surface area – in wall units – is an increasing function of 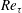 $Re_{\unicode[STIX]{x1D70F}}$. Their size distribution along the three coordinates reveals that, even though in the mean they appear to be circular in the wall-parallel plane, they tend to become more elongated in the spanwise direction after reaching a certain height. Time-tracking of backflow regions in a
$Re_{\unicode[STIX]{x1D70F}}$. Their size distribution along the three coordinates reveals that, even though in the mean they appear to be circular in the wall-parallel plane, they tend to become more elongated in the spanwise direction after reaching a certain height. Time-tracking of backflow regions in a 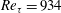 $Re_{\unicode[STIX]{x1D70F}}=934$ simulation showed they convect downstream at the mean velocity corresponding to
$Re_{\unicode[STIX]{x1D70F}}=934$ simulation showed they convect downstream at the mean velocity corresponding to 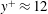 $y^{+}\approx 12$, they seldom interact with other backflow events, their statistical signature extends in the streamwise direction for at least
$y^{+}\approx 12$, they seldom interact with other backflow events, their statistical signature extends in the streamwise direction for at least  $300$ wall units, and they result from a complex interaction between regions of high and low spanwise vorticity far beyond the viscous sublayer. This could explain why some statistical aspects of these near-wall events do not scale in viscous units; they are dependent on the
$300$ wall units, and they result from a complex interaction between regions of high and low spanwise vorticity far beyond the viscous sublayer. This could explain why some statistical aspects of these near-wall events do not scale in viscous units; they are dependent on the 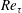 $Re_{\unicode[STIX]{x1D70F}}$-dependent dynamics further away from the wall.
$Re_{\unicode[STIX]{x1D70F}}$-dependent dynamics further away from the wall.
