Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-26T01:25:26.708Z Has data issue: false hasContentIssue false
  • English
  • Français

State estimation in turbulent channel flow from limited observations

Published online by Cambridge University Press:  22 April 2021

Mengze Wang  and
Tamer A. Zaki Open the ORCID record for Tamer A. Zaki [Opens in a new window]
Mengze Wang
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD21218, USA
Tamer A. Zaki*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD21218, USA
*
†Email address for correspondence: t.zaki@jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

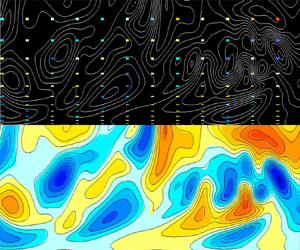
Estimation of the initial state of turbulent channel flow from limited data is investigated using an adjoint-variational approach. The data are generated from a reference direct numerical simulation that is subsampled at different spatiotemporal resolutions. When the velocity data are at 1/4096 the spatiotemporal resolution of the direct numerical simulation, the correlation coefficient between the true and adjoint-variational estimated state exceeds 99 %. The robustness of the algorithm to observation noise is demonstrated. In addition, the impact of the spatiotemporal density of the data on estimation quality is evaluated, and a resolution threshold is established for a successful reconstruction. The critical spanwise data resolution is proportional to the Taylor microscale, which characterizes the domain of dependence of an observation location. Owing to mean advection, either the streamwise or temporal data resolution must satisfy a criterion based on the streamwise Taylor microscale. A second configuration is considered where the subsampled data comprise velocities in the outer layer and wall shear stresses only. The near-wall flow statistics and coherent structures, although not sampled, are accurately reconstructed, which is possible because of the coupling between the outer flow and near-wall motions. Finally, the most challenging configuration is addressed where only the spatiotemporally resolved wall stresses are observed. The estimation remains accurate within the viscous sublayer and deteriorates significantly with distance from the wall. In wall units, this trend is nearly independent of the Reynolds number considered, and is indicative of the fundamental difficulty of reconstructing wall-detached motions from wall data.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 917 , 25 June 2021 , A9
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to ${Re}_{\tau }= 640$. Trans. ASME J. Fluids Engng 126 (5), 835–843.CrossRefGoogle Scholar
Abrahamson, S. & Lonnes, S. 1995 Uncertainty in calculating vorticity from 2D velocity fields using circulation and least-squares approaches. Exp. Fluids 20 (1), 10–20.CrossRefGoogle Scholar
Adrian, R.J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.CrossRefGoogle Scholar
Baars, W.J., Hutchins, N. & Marusic, I. 2016 Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner-outer interaction model. Phys. Rev. Fluids 1, 054406.CrossRefGoogle Scholar
Bardet, P.M., Peterson, P.F. & Savaş, Ö. 2010 Split-screen single-camera stereoscopic PIV application to a turbulent confined swirling layer with free surface. Exp. Fluids 49 (2), 513–524.CrossRefGoogle Scholar
Bewley, T.R. & Protas, B. 2004 Skin friction and pressure: the ‘footprints’ of turbulence. Physica D 196, 28–44.CrossRefGoogle Scholar
Buchta, D.A. & Zaki, T.A. 2020 Observation-infused simulations of high-speed boundary layer transition. J. Fluid Mech. (accepted) arXiv:2011.08265.Google Scholar
Cerizza, D., Sekiguchi, W., Tsukahara, T., Zaki, T.A. & Hasegawa, Y. 2016 Reconstruction of scalar source intensity based on sensor signal in turbulent channel flow. Flow Turbul. Combust. 97 (4), 1211–1233.CrossRefGoogle Scholar
Chandramouli, P., Mémin, E. & Heitz, D. 2020 4D large scale variational data assimilation of a turbulent flow with a dynamics error model. J. Comput. Phys. 412, 109446.CrossRefGoogle Scholar
Chevalier, M., Hœpffner, J., Bewley, T.R. & Henningson, D.S. 2006 State estimation in wall-bounded flow systems. Part 2. Turbulent flows. J. Fluid Mech. 552, 167–187.CrossRefGoogle Scholar
Colburn, C.H., Cessna, J.B. & Bewley, T.R. 2011 State estimation in wall-bounded flow systems. Part 3. The ensemble Kalman filter. J. Fluid Mech. 682, 289–303.CrossRefGoogle Scholar
Constantin, P. & Iyer, G. 2011 A stochastic-Lagrangian approach to the Navier–Stokes equations in domains with boundary. Ann. Probab. 21 (4), 1466–1492.Google Scholar
Deissler, R.G. 1986 Is Navier–Stokes turbulence chaotic? Phys. Fluids 29 (5), 1453–1457.CrossRefGoogle Scholar
Di Leoni, P.C., Mazzino, A. & Biferale, L. 2019 Synchronization to big-data: nudging the Navier–Stokes equations for data assimilation of turbulent flows. arXiv:1905.05860.Google Scholar
Encinar, M.P. & Jiménez, J. 2019 Logarithmic-layer turbulence: a view from the wall. Phys. Rev. Fluids 4 (11), 114603.CrossRefGoogle Scholar
Evensen, G. 1994 Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans 99 (C5), 10143–10162.CrossRefGoogle Scholar
Eyink, G.L., Gupta, A. & Zaki, T.A. 2020 a Stochastic Lagrangian dynamics of vorticity. Part 1. General theory for viscous, incompressible fluids. J. Fluid Mech. 901, A2.CrossRefGoogle Scholar
Eyink, G.L., Gupta, A. & Zaki, T.A. 2020 b Stochastic Lagrangian dynamics of vorticity. Part 2. Application to near-wall channel-flow turbulence. J. Fluid Mech. 901, A3.CrossRefGoogle Scholar
Hamilton, J.M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hœpffner, J., Chevalier, M., Bewley, T.R. & Henningson, D.S. 2005 State estimation in wall-bounded flow systems. Part 1. Perturbed laminar flows. J. Fluid Mech. 534, 263–294.CrossRefGoogle Scholar
Hutchins, N., Hambleton, W.T. & Marusic, I. 2005 Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 541, 21–54.CrossRefGoogle Scholar
Illingworth, S.J., Monty, J.P. & Marusic, I. 2018 Estimating large-scale structures in wall turbulence using linear models. J. Fluid Mech. 842, 146–162.CrossRefGoogle Scholar
Jelly, T.O., Jung, S.Y. & Zaki, T.A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26 (9), 095102.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.CrossRefGoogle Scholar
Jiménez, J. & Moser, R.D. 2007 What are we learning from simulating wall turbulence? Phil. Trans. R. Soc. Lond. A 365 (1852), 715–732.Google ScholarPubMed
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jones, B.L., Heins, P.H., Kerrigan, E.C., Morrison, J.F. & Sharma, A.S. 2015 Modelling for robust feedback control of fluid flows. J. Fluid Mech. 769, 687–722.CrossRefGoogle Scholar
Jones, B.L., Kerrigan, E.C., Morrison, J.F. & Zaki, T.A 2011 Flow estimation of boundary layers using DNS-based wall shear information. Intl J. Control 84 (8), 1310–1325.CrossRefGoogle Scholar
Kim, J. & Bewley, T.R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39 (1), 383–417.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Lalescu, C.C., Meneveau, C. & Eyink, G.L. 2013 Synchronization of chaos in fully developed turbulence. Phys. Rev. Lett. 110 (8), 084102.CrossRefGoogle ScholarPubMed
Law, K., Stuart, A. & Zygalakis, K. 2015 Data Assimilation: A mathematical introduction. Springer.CrossRefGoogle Scholar
Le Dimet, F.-X. & Talagrand, O. 1986 Variational algorithms for analysis and assimilation of meteorological observations: theoretical aspects. Tellus A 38 (2), 97–110.CrossRefGoogle Scholar
Lee, S.J. & Zaki, T.A. 2017 Simulations of natural transition in viscoelastic channel flow. J. Fluid Mech. 820, 232–262.CrossRefGoogle Scholar
Li, Y., Zhang, J., Dong, G. & Abdullah, N.S. 2020 Small-scale reconstruction in three-dimensional Kolmogorov flows using four-dimensional variational data assimilation. J. Fluid Mech. 885, A9.CrossRefGoogle Scholar
Lighthill, M.J. 1963 Boundary layer theory. In Laminar Boundary Layers (ed. L. Rosenhead), pp. 46–113. Oxford University Press.Google Scholar
Liu, Z. & Hasegawa, Y. 2020 Estimation of turbulent channel flow based on time-series wall measurements. Seisan Kenkyu 72 (1), 5–8.Google Scholar
Mao, X., Blackburn, H.M. & Sherwin, S.J. 2013 Calculation of global optimal initial and boundary perturbations for the linearised incompressible Navier–Stokes equations. J. Comput. Phys. 235, 258–273.CrossRefGoogle Scholar
Mao, X., Zaki, T.A., Sherwin, S.J. & Blackburn, H.M. 2017 Transition induced by linear and nonlinear perturbation growth in flow past a compressor blade. J. Fluid Mech. 820, 604–632.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mons, V., Chassaing, J.-C., Gomez, T. & Sagaut, P. 2016 Reconstruction of unsteady viscous flows using data assimilation schemes. J. Comput. Phys. 316, 255–280.CrossRefGoogle Scholar
Mons, V., Chassaing, J.-C. & Sagaut, P. 2017 Optimal sensor placement for variational data assimilation of unsteady flows past a rotationally oscillating cylinder. J. Fluid Mech. 823, 230–277.CrossRefGoogle Scholar
Mons, V., Wang, Q. & Zaki, T.A. 2019 Kriging-enhanced ensemble variational data assimilation for scalar-source identification in turbulent environments. J. Comput. Phys. 398, 108856.CrossRefGoogle Scholar
Moré, J.J. & Thuente, D.J. 1994 Line search algorithms with guaranteed sufficient decrease. ACM Trans. Math. Softw. 20 (3), 286–307.CrossRefGoogle Scholar
Naguib, A.M., Morrison, J.F. & Zaki, T.A. 2010 On the relationship between the wall-shear-stress and transient-growth disturbances in a laminar boundary layer. Phys. Fluids 22 (5), 054103.CrossRefGoogle Scholar
Nikitin, N. 2018 Characteristics of the leading Lyapunov vector in a turbulent channel flow. J. Fluid Mech. 849, 942–967.CrossRefGoogle Scholar
Nocedal, J. 1980 Updating quasi-Newton matrices with limited storage. Math. Comput. 35 (151), 773–782.CrossRefGoogle Scholar
Rosenfeld, M., Kwak, D. & Vinokur, M. 1991 A fractional step solution method for the unsteady incompressible Navier–Stokes equations in generalized coordinate systems. J. Comput. Phys. 94, 102–137.CrossRefGoogle Scholar
Sharma, A.S., Morrison, J.F., McKeon, B.J., Limebeer, D.J.N, Koberg, W.H. & Sherwin, S.J. 2011 Relaminarisation of $Re_{\tau } = 100$ channel flow with globally stabilising linear feedback control. Phys. Fluids 23 (12), 125105.CrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.CrossRefGoogle Scholar
Smits, A.J., McKeon, B.J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.CrossRefGoogle Scholar
Suzuki, T. 2012 Reduced-order Kalman-filtered hybrid simulation combining particle tracking velocimetry and direct numerical simulation. J. Fluid Mech. 709, 249–288.CrossRefGoogle Scholar
Suzuki, T. & Hasegawa, Y. 2017 Estimation of turbulent channel flow at $Re_{\tau }=100$ based on the wall measurement using a simple sequential approach. J. Fluid Mech. 830, 760–796.CrossRefGoogle Scholar
Vishnampet, R., Bodony, D.J. & Freund, J.B. 2015 A practical discrete-adjoint method for high-fidelity compressible turbulence simulations. J. Comput. Phys. 285, 173–192.CrossRefGoogle Scholar
Wang, M., Wang, Q. & Zaki, T.A. 2019 a Discrete adjoint of fractional-step incompressible Navier–Stokes solver in curvilinear coordinates and application to data assimilation. J. Comput. Phys. 396, 427–450.CrossRefGoogle Scholar
Wang, Q., Hasegawa, Y. & Zaki, T.A. 2019 b Spatial reconstruction of steady scalar sources from remote measurements in turbulent flow. J. Fluid Mech. 870, 316–352.CrossRefGoogle Scholar
Yoshida, K., Yamaguchi, J. & Kaneda, Y. 2005 Regeneration of small eddies by data assimilation in turbulence. Phys. Rev. Lett. 94 (1), 014501.CrossRefGoogle ScholarPubMed
Zaki, T.A. 2013 From streaks to spots and on to turbulence: exploring the dynamics of boundary layer transition. Flow Turbul. Combust. 91 (3), 451–473.CrossRefGoogle Scholar
Zaki, T.A. & Durbin, P.A. 2005 Mode interaction and the bypass route to transition. J. Fluid Mech. 531, 85–111.CrossRefGoogle Scholar
Zaki, T.A., Wissink, J.G., Rodi, W. & Durbin, P.A. 2010 Direct numerical simulations of transition in a compressor cascade: the influence of free-stream turbulence. J. Fluid Mech. 665, 57–98.CrossRefGoogle Scholar