Article contents
Stably stratified exact coherent structures in shear flow: the effect of Prandtl number
Published online by Cambridge University Press: 06 November 2019
Abstract
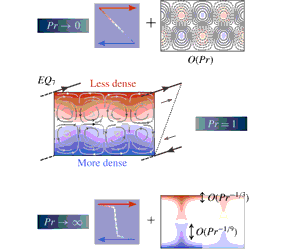
We examine how known unstable equilibria of the Navier–Stokes equations in plane Couette flow adapt to the presence of an imposed stable density difference between the two boundaries for varying values of the Prandtl number  $Pr$, the ratio of viscosity to density diffusivity and fixed moderate Reynolds number,
$Pr$, the ratio of viscosity to density diffusivity and fixed moderate Reynolds number,  $Re=400$. In the two asymptotic limits
$Re=400$. In the two asymptotic limits  $Pr\rightarrow 0$ and
$Pr\rightarrow 0$ and  $Pr\rightarrow \infty$, it is found that such solutions exist at arbitrarily high bulk stratification but for different physical reasons. In the
$Pr\rightarrow \infty$, it is found that such solutions exist at arbitrarily high bulk stratification but for different physical reasons. In the  $Pr\rightarrow 0$ limit, density variations away from a constant stable density gradient become vanishingly small as diffusion of density dominates over advection, allowing equilibria to exist for bulk Richardson number
$Pr\rightarrow 0$ limit, density variations away from a constant stable density gradient become vanishingly small as diffusion of density dominates over advection, allowing equilibria to exist for bulk Richardson number  $\mathit{Ri}_{b}\lesssim O(Re^{-2}Pr^{-1})$. Alternatively, at high Prandtl numbers, density becomes homogenised in the interior by the dominant advection which creates strongly stable stratified boundary layers that recede into the wall as
$\mathit{Ri}_{b}\lesssim O(Re^{-2}Pr^{-1})$. Alternatively, at high Prandtl numbers, density becomes homogenised in the interior by the dominant advection which creates strongly stable stratified boundary layers that recede into the wall as  $Pr\rightarrow \infty$. In this scenario, the density stratification and the flow essentially decouple, thereby mitigating the effect of increasing
$Pr\rightarrow \infty$. In this scenario, the density stratification and the flow essentially decouple, thereby mitigating the effect of increasing  $\mathit{Ri}_{b}$. An asymptotic analysis is presented in the passive scalar regime
$\mathit{Ri}_{b}$. An asymptotic analysis is presented in the passive scalar regime  $\mathit{Ri}_{b}\lesssim O(Re^{-2})$, which reveals
$\mathit{Ri}_{b}\lesssim O(Re^{-2})$, which reveals  $O(Pr^{-1/3})$-thick stratified boundary layers with
$O(Pr^{-1/3})$-thick stratified boundary layers with  $O(Pr^{-2/9})$-wide eruptions, giving rise to density fingers of
$O(Pr^{-2/9})$-wide eruptions, giving rise to density fingers of  $O(Pr^{-1/9})$ length and
$O(Pr^{-1/9})$ length and  $O(Pr^{-4/9})$ width that invade an otherwise homogeneous interior. Finally, increasing
$O(Pr^{-4/9})$ width that invade an otherwise homogeneous interior. Finally, increasing  $Re$ to
$Re$ to  $10^{5}$ in this regime reveals that interior stably stratified density layers can form away from the boundaries, separating well-mixed regions.
$10^{5}$ in this regime reveals that interior stably stratified density layers can form away from the boundaries, separating well-mixed regions.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 6
- Cited by

