Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Espin, M.J.
Quintanilla, M.A.S.
and
Valverde, J.M.
2015.
Effect of particle size polydispersity on the yield stress of magnetofluidized beds as depending on the magnetic field orientation.
Chemical Engineering Journal,
Vol. 277,
Issue. ,
p.
269.
Egorov, Ivan
Egorov, Nikolay
Abbasian Najafabadi, T.
Sevostianov, I.
Yeghiazaryan, K.
Nguyen Dong, A.
and
Mladenovic, V.
2017.
Technological processes intensification in devices with magneto-fluidized bed.
MATEC Web of Conferences,
Vol. 132,
Issue. ,
p.
03001.
Espin, M.J.
Quintanilla, M.A.S.
and
Valverde, J.M.
2017.
Magnetic stabilization of fluidized beds: Effect of magnetic field orientation.
Chemical Engineering Journal,
Vol. 313,
Issue. ,
p.
1335.
Egorov, Ivan N.
Egorov, Nikolay Ya.
Gross, H.-G.
Khaled, H.
Abbasian Najafabadi, T.
Nguyen, D.A.
Kudish, I.
Sevostyanov, I.B.
Cen, Y.G.
Egiazarian, K.
Mladenovic, V.
Karapetyan, G.
and
Minkin, M.
2018.
Influence of electromagnetic effect parameters on ferromagnetic powders fluidity.
MATEC Web of Conferences,
Vol. 226,
Issue. ,
p.
03002.
Ye, Huilin
Shen, Zhiqiang
and
Li, Ying
2018.
Computational modeling of magnetic particle margination within blood flow through LAMMPS.
Computational Mechanics,
Vol. 62,
Issue. 3,
p.
457.
Botello, Francisco Ruiz
Quintanilla, Miguel A.S.
Castellanos, Antonio
Grekova, Elena F.
and
Tournat, Vincent
2018.
Effect of the microstructure on the propagation velocity of ultrasound in magnetic powders.
Ultrasonics,
Vol. 82,
Issue. ,
p.
153.
Espin, M.J.
Quintanilla, M.A.S.
and
Valverde, J.M.
2019.
Effect of temperature on flow properties of magnetofluidized beds at low consolidations.
Chemical Engineering Journal,
Vol. 361,
Issue. ,
p.
50.
Zhu, Quanhong
Li, Hongzhong
Zhu, Qingshan
and
Huang, Qingshan
2019.
Comparing flow regime transition of magnetized fluidized bed with Geldart-B particles between magnetization-FIRST and -LAST operation modes.
Chemical Engineering Journal,
Vol. 360,
Issue. ,
p.
686.
Tschöpe, André
Wyrwoll, Maximilian
Schneider, Michael
Mandel, Karl
and
Franzreb, Matthias
2020.
A magnetically induced fluidized-bed reactor for intensification of electrochemical reactions.
Chemical Engineering Journal,
Vol. 385,
Issue. ,
p.
123845.
Egorov, I N
Egorov, N Ya
and
Egorova, S I
2021.
Stimulated fluidity of Nd-Fe-B powder in magneto fluidized bed.
IOP Conference Series: Materials Science and Engineering,
Vol. 1029,
Issue. 1,
p.
012075.
Zhu, Quanhong
Hao, Weikang
Tao, Jinliang
Huang, Qingshan
and
Yang, Chao
2021.
State dependence of magnetized fluidized bed reactor on operation mode.
Chemical Engineering Journal,
Vol. 407,
Issue. ,
p.
127211.
Zhu, Quanhong
Hao, Weikang
and
Liang, Peng
2021.
Magnetic intensification of mass transfer between fluidizing gas and Geldart-B nonmagnetizable particles: Property effects of added magnetizable particles.
Chemical Engineering Research and Design,
Vol. 175,
Issue. ,
p.
25.
Tao, Jinliang
Hao, Weikang
and
Zhu, Quanhong
2021.
Segregation in magnetized fluidized bed with Geldart-B magnetizable and nonmagnetizable particles.
Chemical Engineering and Processing - Process Intensification,
Vol. 164,
Issue. ,
p.
108421.
Francia, Victor
Wu, Kaiqiao
and
Coppens, Marc-Olivier
2021.
Dynamically structured fluidization: Oscillating the gas flow and other opportunities to intensify gas-solid fluidized bed operation.
Chemical Engineering and Processing - Process Intensification,
Vol. 159,
Issue. ,
p.
108143.
Song, Shulei
Xu, Xuan
Tian, Yakun
and
Chen, Zengqiang
2024.
Study on density distribution characteristics and fine coal separation of magnetically fluidized beds of microfine particles.
International Journal of Coal Preparation and Utilization,
Vol. 44,
Issue. 11,
p.
1864.
Zhang, Qiang
Liu, Wankun
Cao, Yalong
Gai, Hengjun
and
Zhu, Quanhong
2024.
Diverse gas-solid magnetized fluidized beds with different magnetic fields.
Powder Technology,
Vol. 433,
Issue. ,
p.
119241.
Zapater, D.
Kulkarni, S.R.
Wery, F.
Cui, M.
Herguido, J.
Menendez, M.
Heynderickx, G.J.
Van Geem, K.M.
Gascon, J.
and
Castaño, P.
2024.
Multifunctional fluidized bed reactors for process intensification.
Progress in Energy and Combustion Science,
Vol. 105,
Issue. ,
p.
101176.
Wang, Minghao
Wang, Yuqi
Wang, Peng
Huang, Xianhui
Yang, Fuming
Wang, Tong
Du, Jing
and
Yu, Dianyu
2024.
Synthesis and characterization of breast milk analogue structured triacylglycerols by immobilized lipase using magnetic fluidized bed.
LWT,
Vol. 205,
Issue. ,
p.
116561.
Deivendran, Balamurugan
De Somer, Casper
Coene, Annelies
Buelens, Lukas C.
Poelman, Hilde
Galvita, Vladimir V.
Dupre, Luc
Van Geem, Kevin M.
and
Heynderickx, Geraldine J.
2025.
Gas-solid magnetically fluidized beds – A review.
Powder Technology,
Vol. 453,
Issue. ,
p.
120615.
Wang, Jiarui
Wu, Yinglong
Liu, Yang
and
Wang, Simin
2025.
Experimental Study on Inductive Heating Characteristics and Motion Behaviors of Metal Particles under Alternating Magnetic Field.
Industrial & Engineering Chemistry Research,
Vol. 64,
Issue. 23,
p.
11605.
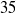 $35$ ,
$35$ , 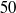 $50$ and
$50$ and 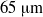 $65~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ particle size. The permeability to gas flow and jamming transition velocity increase with particle size and in a specially marked way when the magnetic field is applied along the gas flow direction. The magnetic contribution to the yield stress is also particularly enhanced for co-flow magnetic fields. However, the effect of particle size on the yield stress shows a dependence on the microstructure packing as affected by particle size and orientation of the field. The magnetic yield stress increases with particle size for magnetic fields applied in the cross-flow configuration while the opposite trend is observed when the direction of the magnetic field is parallel to the gas flow. The observations reported in this paper are generally explained by the formation of chains of particles due to attractive magnetic forces between the magnetized particles and the orientation of these chains with respect to the magnetic field.
$65~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ particle size. The permeability to gas flow and jamming transition velocity increase with particle size and in a specially marked way when the magnetic field is applied along the gas flow direction. The magnetic contribution to the yield stress is also particularly enhanced for co-flow magnetic fields. However, the effect of particle size on the yield stress shows a dependence on the microstructure packing as affected by particle size and orientation of the field. The magnetic yield stress increases with particle size for magnetic fields applied in the cross-flow configuration while the opposite trend is observed when the direction of the magnetic field is parallel to the gas flow. The observations reported in this paper are generally explained by the formation of chains of particles due to attractive magnetic forces between the magnetized particles and the orientation of these chains with respect to the magnetic field.
