Article contents
Stability, sensitivity and optimisation of chaotic acoustic oscillations
Published online by Cambridge University Press: 11 November 2019
Abstract
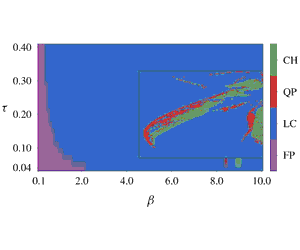
In an acoustic cavity with a heat source, such as a flame in a gas turbine, the thermal energy of the heat source can be converted into acoustic energy, which may generate a loud oscillation. If uncontrolled, these nonlinear acoustic oscillations, also known as thermoacoustic instabilities, can cause large vibrations up to structural failure. Numerical and experimental studies showed that thermoacoustic oscillations can be chaotic. It is not yet known, however, how to minimise such chaotic oscillations. We propose a strategy to analyse and minimise chaotic acoustic oscillations, for which traditional stability and sensitivity methods break down. We investigate the acoustics of a nonlinear heat source in an acoustic resonator. First, we propose covariant Lyapunov analysis as a tool to calculate the stability of chaotic acoustics, making connections with eigenvalue and Floquet analyses. We show that covariant Lyapunov analysis is the most general flow stability tool. Second, covariant Lyapunov vector analysis is applied to a chaotic system. The time-averaged acoustic energy is investigated by varying the heat-source parameters. Thermoacoustic systems can display both hyperbolic and non-hyperbolic chaos, as well as discontinuities in the time-averaged acoustic energy. Third, we embed sensitivities of the time-averaged acoustic energy in an optimisation routine. This procedure achieves a significant reduction in acoustic energy and identifies the bifurcations to chaos. The analysis and methods proposed enable the reduction of chaotic oscillations in thermoacoustic systems by optimal passive control. The techniques presented can be used in other unsteady fluid-dynamics problems with virtually no modification.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 30
- Cited by

