Article contents
Stability of the anabatic Prandtl slope flow in a stably stratified medium
Published online by Cambridge University Press: 18 December 2019
Abstract
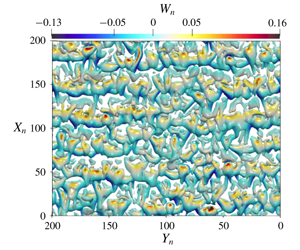
In the Prandtl model for anabatic slope flows, a uniform positive buoyancy flux at the surface drives an upslope flow against a stable background stratification. In the present study, we conduct linear stability analysis of the anabatic slope flow under this model and contrast it against the katabatic case as presented in Xiao & Senocak (J. Fluid Mech., vol. 865, 2019, R2). We show that the buoyancy component normal to the sloped surface is responsible for the emergence of stationary longitudinal rolls, whereas a generalised Kelvin–Helmholtz (KH) type of mechanism consisting of shear instability modulated by buoyancy results in a streamwise-travelling mode. In the anabatic case, for slope angles larger than  $9^{\circ }$ to the horizontal, the travelling KH mode is dominant whereas, at lower inclination angles, the formation of the stationary vortex instability is favoured. The same dynamics holds qualitatively for the katabatic case, but the mode transition appears at slope angles of approximately
$9^{\circ }$ to the horizontal, the travelling KH mode is dominant whereas, at lower inclination angles, the formation of the stationary vortex instability is favoured. The same dynamics holds qualitatively for the katabatic case, but the mode transition appears at slope angles of approximately  $62^{\circ }$. For a fixed slope angle and Prandtl number, we demonstrate through asymptotic analysis of linear growth rates that it is possible to devise a classification scheme that demarcates the stability of Prandtl slope flows into distinct regimes based on the dimensionless stratification perturbation number. We verify the existence of the instability modes with the help of direct numerical simulations, and observe close agreements between simulation results and predictions of linear analysis. For slope angle values in the vicinity of the junction point in the instability map, both longitudinal rolls and travelling waves coexist simultaneously and form complex flow structures.
$62^{\circ }$. For a fixed slope angle and Prandtl number, we demonstrate through asymptotic analysis of linear growth rates that it is possible to devise a classification scheme that demarcates the stability of Prandtl slope flows into distinct regimes based on the dimensionless stratification perturbation number. We verify the existence of the instability modes with the help of direct numerical simulations, and observe close agreements between simulation results and predictions of linear analysis. For slope angle values in the vicinity of the junction point in the instability map, both longitudinal rolls and travelling waves coexist simultaneously and form complex flow structures.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 7
- Cited by

