Article contents
Stability of a moving radial liquid sheet: experiments
Published online by Cambridge University Press: 08 April 2015
Abstract
A recent theory (Tirumkudulu & Paramati, Phys. Fluids, vol. 25, 2013, 102107) for a radially expanding liquid sheet, that accounts for liquid inertia, interfacial tension and thinning of the liquid sheet while ignoring the inertia of the surrounding gas and viscous effects, shows that such a sheet is convectively unstable to small sinuous disturbances at all frequencies and Weber numbers 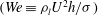 $(We\equiv {\it\rho}_{l}U^{2}h/{\it\sigma})$ . Here,
$(We\equiv {\it\rho}_{l}U^{2}h/{\it\sigma})$ . Here, 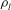 ${\it\rho}_{l}$ and
${\it\rho}_{l}$ and  ${\it\sigma}$ are the density and surface tension of the liquid, respectively,
${\it\sigma}$ are the density and surface tension of the liquid, respectively, 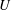 $U$ is the speed of the liquid jet, and
$U$ is the speed of the liquid jet, and 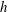 $h$ is the local sheet thickness. In this study we use a simple non-contact optical technique based on laser-induced fluorescence (LIF) to measure the instantaneous local sheet thickness and displacement of a circular sheet produced by head-on impingement of two laminar jets. When the impingement point is disturbed via acoustic forcing, sinuous waves produced close to the impingement point travel radially outwards. The phase speed of the sinuous wave decreases while the amplitude grows as they propagate radially outwards. Our experimental technique was unable to detect thickness modulations in the presence of forcing, suggesting that the modulations could be smaller than the resolution of our experimental technique. The measured phase speed of the sinuous wave envelope matches with theoretical predictions while there is a qualitative agreement in the case of spatial growth. We show that there is a range of frequencies over which the sheet is unstable due to both aerodynamic interaction and thinning effects, while outside this range, thinning effects dominate. These results imply that a full theory that describes the dynamics of a radially expanding liquid sheet should account for both effects.
$h$ is the local sheet thickness. In this study we use a simple non-contact optical technique based on laser-induced fluorescence (LIF) to measure the instantaneous local sheet thickness and displacement of a circular sheet produced by head-on impingement of two laminar jets. When the impingement point is disturbed via acoustic forcing, sinuous waves produced close to the impingement point travel radially outwards. The phase speed of the sinuous wave decreases while the amplitude grows as they propagate radially outwards. Our experimental technique was unable to detect thickness modulations in the presence of forcing, suggesting that the modulations could be smaller than the resolution of our experimental technique. The measured phase speed of the sinuous wave envelope matches with theoretical predictions while there is a qualitative agreement in the case of spatial growth. We show that there is a range of frequencies over which the sheet is unstable due to both aerodynamic interaction and thinning effects, while outside this range, thinning effects dominate. These results imply that a full theory that describes the dynamics of a radially expanding liquid sheet should account for both effects.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 14
- Cited by


