Article contents
The stability and nonlinear evolution of quasi-geostrophic toroidal vortices
Published online by Cambridge University Press: 22 January 2019
Abstract
We investigate the linear stability and nonlinear evolution of a three-dimensional toroidal vortex of uniform potential vorticity under the quasi-geostrophic approximation. The torus can undergo a primary instability leading to the formation of a circular array of vortices, whose radius is approximately the same as the major radius of the torus. This occurs for azimuthal instability mode numbers 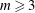 $m\geqslant 3$, on sufficiently thin tori. The number of vortices corresponds to the azimuthal mode number of the most unstable mode growing on the torus. This value of
$m\geqslant 3$, on sufficiently thin tori. The number of vortices corresponds to the azimuthal mode number of the most unstable mode growing on the torus. This value of 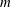 $m$ depends on the ratio of the torus’ major radius to its minor radius, with thin tori favouring high mode
$m$ depends on the ratio of the torus’ major radius to its minor radius, with thin tori favouring high mode 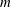 $m$ values. The resulting array is stable when
$m$ values. The resulting array is stable when 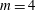 $m=4$ and
$m=4$ and 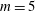 $m=5$ and unstable when
$m=5$ and unstable when 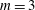 $m=3$ and
$m=3$ and 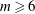 $m\geqslant 6$. When
$m\geqslant 6$. When 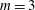 $m=3$ the array has barely formed before it collapses towards its centre with the ejection of filamentary debris. When
$m=3$ the array has barely formed before it collapses towards its centre with the ejection of filamentary debris. When 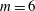 $m=6$ the vortices exhibit oscillatory staggering, and when
$m=6$ the vortices exhibit oscillatory staggering, and when 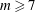 $m\geqslant 7$ they exhibit irregular staggering followed by substantial vortex migration, e.g. of one vortex to the centre when
$m\geqslant 7$ they exhibit irregular staggering followed by substantial vortex migration, e.g. of one vortex to the centre when 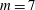 $m=7$. We also investigate the effect of an additional vortex located at the centre of the torus. This vortex alters the stability properties of the torus as well as the stability properties of the circular vortex array formed from the primary toroidal instability. We show that a like-signed central vortex may stabilise a circular
$m=7$. We also investigate the effect of an additional vortex located at the centre of the torus. This vortex alters the stability properties of the torus as well as the stability properties of the circular vortex array formed from the primary toroidal instability. We show that a like-signed central vortex may stabilise a circular 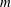 $m$-vortex array with
$m$-vortex array with 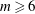 $m\geqslant 6$.
$m\geqslant 6$.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 12
- Cited by
Linked content
Please note that this article has a (1).

