Article contents
Spectral broadening and flow randomization in free shear layers
Published online by Cambridge University Press: 06 July 2012
Abstract
It has been observed experimentally that when a free shear layer is perturbed by a disturbance consisting of two waves with frequencies 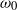 and
and 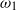 , components with the combination frequencies
, components with the combination frequencies 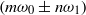 (
(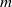 and
and  being integers) develop to a significant level thereby causing flow randomization. This spectral broadening process is investigated theoretically for the case where the frequency difference
being integers) develop to a significant level thereby causing flow randomization. This spectral broadening process is investigated theoretically for the case where the frequency difference 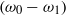 is small, so that the perturbation can be treated as a modulated wavetrain. A nonlinear evolution system governing the spectral dynamics is derived by using the non-equilibrium nonlinear critical layer approach. The formulation provides an appropriate mathematical description of the physical concepts of sideband instability and amplitude–phase modulation, which were suggested by experimentalists. Numerical solutions of the nonlinear evolution system indicate that the present theory captures measurements and observations rather well.
is small, so that the perturbation can be treated as a modulated wavetrain. A nonlinear evolution system governing the spectral dynamics is derived by using the non-equilibrium nonlinear critical layer approach. The formulation provides an appropriate mathematical description of the physical concepts of sideband instability and amplitude–phase modulation, which were suggested by experimentalists. Numerical solutions of the nonlinear evolution system indicate that the present theory captures measurements and observations rather well.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 11
- Cited by

