Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wilczek, Michael
Stevens, Richard J.A.M.
and
Meneveau, Charles
2015.
Height-dependence of spatio-temporal spectra of wall-bounded turbulence – LES results and model predictions.
Journal of Turbulence,
Vol. 16,
Issue. 10,
p.
937.
de Kat, Roeland
and
Ganapathisubramani, Bharathram
2015.
Frequency–wavenumber mapping in turbulent shear flows.
Journal of Fluid Mechanics,
Vol. 783,
Issue. ,
p.
166.
Anderson, William
2016.
Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations.
Journal of Fluid Mechanics,
Vol. 789,
Issue. ,
p.
567.
Ghate, Aditya S.
and
Lele, Sanjiva K.
2016.
Multiscale Kinematic Simulations of the Stratified Surface Layer and interactions with wind turbine arrays.
Katul, Gabriel G.
Banerjee, Tirtha
Cava, Daniela
Germano, Massimo
and
Porporato, Amilcare
2016.
Generalized logarithmic scaling for high-order moments of the longitudinal velocity component explained by the random sweeping decorrelation hypothesis.
Physics of Fluids,
Vol. 28,
Issue. 9,
Drivas, Theodore D.
Johnson, Perry L.
Lalescu, Cristian C.
and
Wilczek, Michael
2017.
Large-scale sweeping of small-scale eddies in turbulence: A filtering approach.
Physical Review Fluids,
Vol. 2,
Issue. 10,
Bossuyt, Juliaan
Meneveau, Charles
and
Meyers, Johan
2017.
Wind farm power fluctuations and spatial sampling of turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
329.
Wang, C.
Tang, Z.
Bristow, N.
Blois, G.
Christensen, K.T.
and
Anderson, W.
2017.
Numerical and experimental study of flow over stages of an offset merger dune interaction.
Computers & Fluids,
Vol. 158,
Issue. ,
p.
72.
Cheng, Yu
Sayde, Chadi
Li, Qi
Basara, Jeffrey
Selker, John
Tanner, Evan
and
Gentine, Pierre
2017.
Failure of Taylor's hypothesis in the atmospheric surface layer and its correction for eddy‐covariance measurements.
Geophysical Research Letters,
Vol. 44,
Issue. 9,
p.
4287.
Yang, X. I. A.
Baidya, R.
Johnson, P.
Marusic, I.
and
Meneveau, C.
2017.
Structure function tensor scaling in the logarithmic region derived from the attached eddy model of wall-bounded turbulent flows.
Physical Review Fluids,
Vol. 2,
Issue. 6,
He, Guowei
Jin, Guodong
and
Yang, Yue
2017.
Space-Time Correlations and Dynamic Coupling in Turbulent Flows.
Annual Review of Fluid Mechanics,
Vol. 49,
Issue. 1,
p.
51.
Bandi, M. M.
2017.
Spectrum of Wind Power Fluctuations.
Physical Review Letters,
Vol. 118,
Issue. 2,
Zhu, Xiaowei
Iungo, G. Valerio
Leonardi, Stefano
and
Anderson, William
2017.
Parametric Study of Urban-Like Topographic Statistical Moments Relevant to a Priori Modelling of Bulk Aerodynamic Parameters.
Boundary-Layer Meteorology,
Vol. 162,
Issue. 2,
p.
231.
Wu, Ting
Geng, Chenhui
Yao, Yichen
Xu, Chunxiao
and
He, Guowei
2017.
Characteristics of space-time energy spectra in turbulent channel flows.
Physical Review Fluids,
Vol. 2,
Issue. 8,
Ghate, Aditya S.
and
Lele, Sanjiva K.
2017.
Subfilter-scale enrichment of planetary boundary layer large eddy simulation using discrete Fourier–Gabor modes.
Journal of Fluid Mechanics,
Vol. 819,
Issue. ,
p.
494.
Squire, D. T.
Hutchins, N.
Morrill-Winter, C.
Schultz, M. P.
Klewicki, J. C.
and
Marusic, I.
2017.
Applicability of Taylor’s hypothesis in rough- and smooth-wall boundary layers.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
398.
Sagaut, Pierre
and
Cambon, Claude
2018.
Homogeneous Turbulence Dynamics.
p.
439.
Anderson, William
Yang, Jianzhi
Shrestha, Kalyan
and
Awasthi, Ankit
2018.
Turbulent secondary flows in wall turbulence: vortex forcing, scaling arguments, and similarity solution.
Environmental Fluid Mechanics,
Vol. 18,
Issue. 6,
p.
1351.
Lukassen, Laura J.
Stevens, Richard J. A. M.
Meneveau, Charles
and
Wilczek, Michael
2018.
Modeling space‐time correlations of velocity fluctuations in wind farms.
Wind Energy,
Vol. 21,
Issue. 7,
p.
474.
Awasthi, Ankit
and
Anderson, William
2018.
Numerical study of turbulent channel flow perturbed by spanwise topographic heterogeneity: Amplitude and frequency modulation within low- and high-momentum pathways.
Physical Review Fluids,
Vol. 3,
Issue. 4,
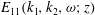 $E_{11}(k_{1},k_{2},{\it\omega};z)$ , where
$E_{11}(k_{1},k_{2},{\it\omega};z)$ , where 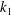 $k_{1}$ ,
$k_{1}$ ,  $k_{2}$ are the streamwise and spanwise wavenumbers,
$k_{2}$ are the streamwise and spanwise wavenumbers, 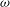 ${\it\omega}$ is the frequency and
${\it\omega}$ is the frequency and  $z$ is the distance to the wall. The results are found to be in good agreement with LES data.
$z$ is the distance to the wall. The results are found to be in good agreement with LES data.

