Article contents
Spanwise oscillatory wall motion in channel flow: drag-reduction mechanisms inferred from DNS-predicted phase-wise property variations at  $\textit {Re}_{\boldsymbol {\boldsymbol{\tau}}} =1000$
$\textit {Re}_{\boldsymbol {\boldsymbol{\tau}}} =1000$
Published online by Cambridge University Press: 10 March 2014
Abstract
A direct-numerical-simulation-based study is presented, which focuses on the response of near-wall turbulence and skin friction to the imposition of an oscillatory spanwise wall motion in channel flow. One point of contrast to earlier studies is the relatively high Reynolds number of the flow, namely 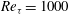 $Re_\tau =1000$ in the unforced baseline flow. Another is the focus on transients in the drag that are in the form of moderate oscillatory variations in the skin friction and near-wall turbulence around the low-drag state at a sub-optimal actuation period. These conditions allow phase-averaged statistics to be extracted, during the periodic drag decrease and rise, that shed light on the interaction between turbulence and the unsteady Stokes strain. Results are presented for, among others, the phase-averaged second moments of stochastic fluctuations and their budgets, enstrophy components and joint probability density functions. The study identifies velocity skewness – the wall-normal derivative of the angle of the velocity vector – as playing a significant role in the streak-damping process during the drag-reduction phase. Furthermore, the phase-wise asymmetry in the skewness is identified as the source of a distinctive hysteresis in all properties, wherein the drag decrease progresses over a longer proportion of the actuation cycle than the drag increase. This feature, coupled with the fact that the streak-generation time scale limits the ability of the streaks to re-establish themselves during the low-skewness phase when the actuation period is sufficiently short, is proposed to drive the drag-reduction process. The observations in the study thus augment a previously identified mechanism proposed by two of the present authors, in which the drag-reduction process was linked to the rate of change in the Stokes strain in the upper region of the viscous sublayer where the streaks are strongest. Furthermore, an examination of the stochastic-stress budgets and the enstrophy lead to conclusions contrasting with those recently proposed by other authors, according to which the drag-reduction process is linked to increases in enstrophy and turbulence-energy dissipation. It is shown, both for the transient drag-reduction phase and theperiodic drag fluctuations around the low-drag state, that the drag decrease/increase phases are correlated with decreases/increases in both enstrophy and dissipation.
$Re_\tau =1000$ in the unforced baseline flow. Another is the focus on transients in the drag that are in the form of moderate oscillatory variations in the skin friction and near-wall turbulence around the low-drag state at a sub-optimal actuation period. These conditions allow phase-averaged statistics to be extracted, during the periodic drag decrease and rise, that shed light on the interaction between turbulence and the unsteady Stokes strain. Results are presented for, among others, the phase-averaged second moments of stochastic fluctuations and their budgets, enstrophy components and joint probability density functions. The study identifies velocity skewness – the wall-normal derivative of the angle of the velocity vector – as playing a significant role in the streak-damping process during the drag-reduction phase. Furthermore, the phase-wise asymmetry in the skewness is identified as the source of a distinctive hysteresis in all properties, wherein the drag decrease progresses over a longer proportion of the actuation cycle than the drag increase. This feature, coupled with the fact that the streak-generation time scale limits the ability of the streaks to re-establish themselves during the low-skewness phase when the actuation period is sufficiently short, is proposed to drive the drag-reduction process. The observations in the study thus augment a previously identified mechanism proposed by two of the present authors, in which the drag-reduction process was linked to the rate of change in the Stokes strain in the upper region of the viscous sublayer where the streaks are strongest. Furthermore, an examination of the stochastic-stress budgets and the enstrophy lead to conclusions contrasting with those recently proposed by other authors, according to which the drag-reduction process is linked to increases in enstrophy and turbulence-energy dissipation. It is shown, both for the transient drag-reduction phase and theperiodic drag fluctuations around the low-drag state, that the drag decrease/increase phases are correlated with decreases/increases in both enstrophy and dissipation.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 79
- Cited by

