Article contents
Slender-body approximations for advection–diffusion problems
Published online by Cambridge University Press: 06 March 2015
Abstract
We consider steady advection–diffusion about a slender body of revolution at arbitrary 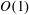 $O(1)$ Péclet numbers (
$O(1)$ Péclet numbers ( 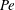 $\mathit{Pe}$ ). The transported scalar attenuates at large distances and is governed by axisymmetric (either Dirichlet or Neumann) data prescribed at the body boundary. The advecting field is assumed to be an axisymmetric Stokes flow approaching a uniform stream at large distances and satisfying impermeability at the boundary; otherwise, the interfacial distribution of tangential velocity is assumed to be arbitrary, irrotational and no-slip Stokes flows being particular cases. Employing the method of matched asymptotic expansions, we develop a systematic scheme for the calculation of the scalar concentration in increasing powers of
$\mathit{Pe}$ ). The transported scalar attenuates at large distances and is governed by axisymmetric (either Dirichlet or Neumann) data prescribed at the body boundary. The advecting field is assumed to be an axisymmetric Stokes flow approaching a uniform stream at large distances and satisfying impermeability at the boundary; otherwise, the interfacial distribution of tangential velocity is assumed to be arbitrary, irrotational and no-slip Stokes flows being particular cases. Employing the method of matched asymptotic expansions, we develop a systematic scheme for the calculation of the scalar concentration in increasing powers of 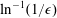 $\ln ^{-1}(1/{\it\epsilon})$ ,
$\ln ^{-1}(1/{\it\epsilon})$ , 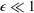 ${\it\epsilon}\ll 1$ being the body’s characteristic thickness to length ratio. The leading term in the inner expansion coincides with the pure diffusion case, the second term depends nonlinearly on the magnitude of the far-field stream and higher-order terms depend on the boundary distribution of tangential velocity. In the special case of irrotational flow and Neumann boundary conditions the logarithmic expansion terminates, leaving an algebraic error in
${\it\epsilon}\ll 1$ being the body’s characteristic thickness to length ratio. The leading term in the inner expansion coincides with the pure diffusion case, the second term depends nonlinearly on the magnitude of the far-field stream and higher-order terms depend on the boundary distribution of tangential velocity. In the special case of irrotational flow and Neumann boundary conditions the logarithmic expansion terminates, leaving an algebraic error in  ${\it\epsilon}$ . The general formulae developed can be directly applied to numerous physical scenarios. We here consider the classical problem of forced heat convection from an isothermal body, finding a two-term expansion for
${\it\epsilon}$ . The general formulae developed can be directly applied to numerous physical scenarios. We here consider the classical problem of forced heat convection from an isothermal body, finding a two-term expansion for 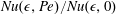 $\mathit{Nu}({\it\epsilon},\mathit{Pe})/\mathit{Nu}({\it\epsilon},0)$ , the ratio of the Nusselt number to its value at
$\mathit{Nu}({\it\epsilon},\mathit{Pe})/\mathit{Nu}({\it\epsilon},0)$ , the ratio of the Nusselt number to its value at 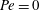 $\mathit{Pe}=0$ . This ratio is insensitive to the particle shape at the asymptotic orders considered; at moderately large
$\mathit{Pe}=0$ . This ratio is insensitive to the particle shape at the asymptotic orders considered; at moderately large 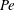 $\mathit{Pe}$ (
$\mathit{Pe}$ ( 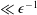 $\ll {\it\epsilon}^{-1}$ ) its deviation from unity is
$\ll {\it\epsilon}^{-1}$ ) its deviation from unity is 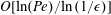 $O[\ln (\mathit{Pe})/\text{ln}\,(1/{\it\epsilon})]$ , marking the poor effectiveness of advection about slender bodies. The expansion is compared with a numerical computation in the case of a prolate spheroid in both irrotational and no-slip Stokes flows.
$O[\ln (\mathit{Pe})/\text{ln}\,(1/{\it\epsilon})]$ , marking the poor effectiveness of advection about slender bodies. The expansion is compared with a numerical computation in the case of a prolate spheroid in both irrotational and no-slip Stokes flows.
Information
- Type
- Rapids
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 6
- Cited by


