Article contents
A slender drop in a nonlinear extensional flow
Published online by Cambridge University Press: 02 November 2016
Abstract
The deformation of a slender drop in a nonlinear axisymmetric extensional and creeping flow has been theoretically studied. This problem, which was first suggested by Sherwood (J. Fluid Mech., vol. 144, 1984, pp. 281–295), is being revisited, and new results are presented. The problem is governed by three dimensionless parameters: the capillary number ( 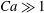 $\mathit{Ca}\gg 1$ ), the viscosity ratio (
$\mathit{Ca}\gg 1$ ), the viscosity ratio ( 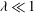 $\unicode[STIX]{x1D706}\ll 1$ ), and the nonlinear intensity of the flow (
$\unicode[STIX]{x1D706}\ll 1$ ), and the nonlinear intensity of the flow ( 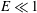 $E\ll 1$ ). Contrary to linear extensional flow (
$E\ll 1$ ). Contrary to linear extensional flow ( 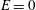 $E=0$ ), where the local radius of the drop decreases monotonically (in the positive
$E=0$ ), where the local radius of the drop decreases monotonically (in the positive  $z$ direction), in a nonlinear extensional flow (
$z$ direction), in a nonlinear extensional flow ( 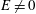 $E\neq 0$ ), two possible steady shapes exist: steady shapes (stable or unstable) with the local radius decreasing monotonically, and steady shapes (unstable) where the local radius of the drop has a local maximum, besides the one at the centre of the drop. Similar to linear extensional flow, the addition of nonlinear extensional effects does not change the end shape of the steady drop, which has pointed ends. A stability analysis has been done to distinguish between stable and unstable steady shapes and to determine the breakup point. Time-dependent studies reveal three types of breakup mechanism: a centre pinching mode, indefinite elongation, and a mechanism that remind us of tip-streaming, where a cusp is developed at the end of the drop.
$E\neq 0$ ), two possible steady shapes exist: steady shapes (stable or unstable) with the local radius decreasing monotonically, and steady shapes (unstable) where the local radius of the drop has a local maximum, besides the one at the centre of the drop. Similar to linear extensional flow, the addition of nonlinear extensional effects does not change the end shape of the steady drop, which has pointed ends. A stability analysis has been done to distinguish between stable and unstable steady shapes and to determine the breakup point. Time-dependent studies reveal three types of breakup mechanism: a centre pinching mode, indefinite elongation, and a mechanism that remind us of tip-streaming, where a cusp is developed at the end of the drop.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 12
- Cited by


