Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tyliszczak, Artur
2018.
Parametric study of multi-armed jets.
International Journal of Heat and Fluid Flow,
Vol. 73,
Issue. ,
p.
82.
Gohil, Trushar B.
and
Saha, Arun K.
2019.
Numerical simulation of forced circular jets: Effect of flapping perturbation.
Physics of Fluids,
Vol. 31,
Issue. 8,
Boguslawski, A.
Wawrzak, K.
and
Tyliszczak, A.
2019.
A new insight into understanding the Crow and Champagne preferred mode: a numerical study.
Journal of Fluid Mechanics,
Vol. 869,
Issue. ,
p.
385.
Tyliszczak, Artur
and
Geurts, Bernard J.
2019.
Controlling spatio-temporal evolution of natural and excited square jets via inlet conditions.
International Journal of Heat and Fluid Flow,
Vol. 80,
Issue. ,
p.
108488.
Wu, M.
Xu, M.
Mi, J.
and
Deo, R.C.
2020.
Mixing characteristics of a film-exciting flapping jet.
International Journal of Heat and Fluid Flow,
Vol. 82,
Issue. ,
p.
108532.
Worth, Nicholas A.
Mistry, Dhiren
Berk, Tim
and
Dawson, James R.
2020.
Vortex dynamics of a jet at the pressure node in a standing wave.
Journal of Fluid Mechanics,
Vol. 882,
Issue. ,
Shaabani-Ardali, Léopold
Sipp, Denis
and
Lesshafft, Lutz
2020.
Optimal triggering of jet bifurcation: an example of optimal forcing applied to a time-periodic base flow.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Dave, Sagar
Anghan, Chetankumar
Saincher, Shaswat
and
Banerjee, Jyotirmay
2021.
Direct numerical simulation of forced turbulent round jet: Effect of flow confinement and varicose excitation.
Physics of Fluids,
Vol. 33,
Issue. 7,
Shahsavari, Mohammad
Wang, Bing
Zhang, Bo
Jiang, Guanyu
and
Zhao, Dan
2021.
Response of supercritical round jets to various excitation modes.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Ahmed, Shady E.
San, Omer
Kara, Kursat
Younis, Rami
Rasheed, Adil
and
Tian, Fang-Bao
2021.
Multifidelity computing for coupling full and reduced order models.
PLOS ONE,
Vol. 16,
Issue. 2,
p.
e0246092.
Wawrzak, Karol
Boguslawski, Andrzej
and
Tyliszczak, Artur
2021.
A Numerical Study of the Global Instability in Counter-Current Homogeneous Density Incompressible Round Jets.
Flow, Turbulence and Combustion,
Vol. 107,
Issue. 4,
p.
901.
Shevchenko, A. K.
and
Yakovenko, S. N.
2021.
Numerical models of flow control in jets.
Vol. 2351,
Issue. ,
p.
040045.
Æsøy, Eirik
Aguilar, José G.
Worth, Nicholas A.
and
Dawson, James R.
2021.
The response of an axisymmetric jet placed at various positions in a standing wave.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Shevchenko, A. K.
and
Yakovenko, S. N.
2021.
Numerical study of flow control methods and splitting effects in a round submerged jet.
Thermophysics and Aeromechanics,
Vol. 28,
Issue. 3,
p.
353.
Tyliszczak, Artur
and
Wawrzak, Agnieszka
2022.
A numerical study of a lifted $$\hbox {H}_2/\hbox {N}_2$$ flame excited by an axial and flapping forcing.
Scientific Reports,
Vol. 12,
Issue. 1,
Tyliszczak, Artur
Kuban, Lukasz
and
Stempka, Jakub
2022.
Numerical analysis of non-excited and excited jets issuing from non-circular nozzles.
International Journal of Heat and Fluid Flow,
Vol. 94,
Issue. ,
p.
108944.
Wu, Mengwei
Li, Chunwei
Zhu, Chuanqing
Wang, Guochang
Xu, Minyi
and
Mi, Jianchun
2022.
On flapping jets induced by a fluttering film and from circular nozzles of smooth contraction, orifice plate and long pipe.
Experiments in Fluids,
Vol. 63,
Issue. 5,
Wawrzak, Agnieszka
Wawrzak, Karol
Boguslawski, Andrzej
Tyliszczak, Artur
and
Geurts, Bernard J.
2023.
Global instability phenomenon as a physical mechanism controlling dynamics of a nitrogen-diluted hydrogen flame.
International Journal of Heat and Mass Transfer,
Vol. 213,
Issue. ,
p.
124260.
Tsujimoto, Koichi
Banno, Y.
Ando, Toshitake
and
Takahashi, M.
2023.
Flow and heat transfer characteristics of impinging jets controlled with rotating inclined jet using direct numerical simulation
.
p.
12.
Tsujimoto, Koichi
Banno, Y.
Ando, Toshitake
and
Takahashi, M.
2023.
Flow and heat transfer characteristics of impinging jets controlled with rotating inclined jet using direct numerical simulation
.
p.
12.
 $0.45<\mathit{St}_{D}<0.525$ , with an excitation frequency ratio range of
$0.45<\mathit{St}_{D}<0.525$ , with an excitation frequency ratio range of 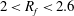 $2<R_{f}<2.6$ , for which blooming jets are formed. The role of inlet shear layer thickness is less important as far as the blooming jet is concerned, while increasing excitation amplitude increases entrainment. Time-averaged data show that the blooming patterns persist in time, showing a substantial increase in spreading and entrainment.
$2<R_{f}<2.6$ , for which blooming jets are formed. The role of inlet shear layer thickness is less important as far as the blooming jet is concerned, while increasing excitation amplitude increases entrainment. Time-averaged data show that the blooming patterns persist in time, showing a substantial increase in spreading and entrainment.

