Article contents
Simply-connected vortex-patch shallow-water quasi-equilibria
Published online by Cambridge University Press: 05 March 2014
Abstract
We examine the form, properties, stability and evolution of simply-connected vortex-patch relative quasi-equilibria in the single-layer 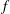 $f$ -plane shallow-water model of geophysical fluid dynamics. We examine the effects of the size, shape and strength of vortices in this system, represented by three distinct parameters completely describing the families of the quasi-equilibria. Namely, these are the ratio
$f$ -plane shallow-water model of geophysical fluid dynamics. We examine the effects of the size, shape and strength of vortices in this system, represented by three distinct parameters completely describing the families of the quasi-equilibria. Namely, these are the ratio 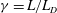 $\gamma = L/L_D$ between the horizontal size of the vortices and the Rossby deformation length; the aspect ratio
$\gamma = L/L_D$ between the horizontal size of the vortices and the Rossby deformation length; the aspect ratio 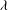 $\lambda $ between the minor to major axes of the vortex; and a potential vorticity (PV)-based Rossby number
$\lambda $ between the minor to major axes of the vortex; and a potential vorticity (PV)-based Rossby number 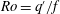 $\mathit{Ro}= q^{\prime }/f$ , the ratio of the PV anomaly
$\mathit{Ro}= q^{\prime }/f$ , the ratio of the PV anomaly 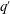 $q^{\prime }$ within the vortex to the Coriolis frequency
$q^{\prime }$ within the vortex to the Coriolis frequency 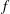 $f$ . By defining an appropriate steadiness parameter, we find that the quasi-equilibria remain steady for long times, enabling us to determine the boundary of stability
$f$ . By defining an appropriate steadiness parameter, we find that the quasi-equilibria remain steady for long times, enabling us to determine the boundary of stability 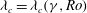 $\lambda _c=\lambda _c(\gamma ,\mathit{Ro})$ , for
$\lambda _c=\lambda _c(\gamma ,\mathit{Ro})$ , for 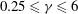 $0.25 \leq \gamma \leq 6$ and
$0.25 \leq \gamma \leq 6$ and 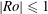 $\delimiter "026A30C \mathit{Ro}\delimiter "026A30C \leq 1$ . By calling two states which share
$\delimiter "026A30C \mathit{Ro}\delimiter "026A30C \leq 1$ . By calling two states which share 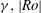 $\gamma ,\delimiter "026A30C \mathit{Ro}\delimiter "026A30C $ and
$\gamma ,\delimiter "026A30C \mathit{Ro}\delimiter "026A30C $ and 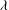 $\lambda $ ‘equivalent’, we find a clear asymmetry in the stability of cyclonic (
$\lambda $ ‘equivalent’, we find a clear asymmetry in the stability of cyclonic ( 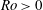 $\mathit{Ro}> 0$ ) and anticyclonic (
$\mathit{Ro}> 0$ ) and anticyclonic ( 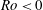 $\mathit{Ro}<0$ ) equilibria, with cyclones being able to sustain greater deformations than anticyclones before experiencing an instability. We find that ageostrophic motions stabilise cyclones and destabilise anticyclones. Both types of vortices undergo the same main types of unstable evolution, albeit in different ranges of the parameter space, (a) vacillations for large-
$\mathit{Ro}<0$ ) equilibria, with cyclones being able to sustain greater deformations than anticyclones before experiencing an instability. We find that ageostrophic motions stabilise cyclones and destabilise anticyclones. Both types of vortices undergo the same main types of unstable evolution, albeit in different ranges of the parameter space, (a) vacillations for large- 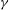 $\gamma $ , large-
$\gamma $ , large-  $\mathit{Ro}$ states, (b) filamentation for small-
$\mathit{Ro}$ states, (b) filamentation for small- 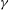 $\gamma $ states and (c) vortex splitting, asymmetric for intermediate-
$\gamma $ states and (c) vortex splitting, asymmetric for intermediate- 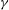 $\gamma $ and symmetric for large-
$\gamma $ and symmetric for large- 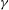 $\gamma $ states.
$\gamma $ states.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 2
- Cited by

