Article contents
A simple and practical model for combined wave–current canopy flows
Published online by Cambridge University Press: 24 February 2015
Abstract
Laboratory experiments were used to evaluate and improve modelling of combined wave–current flow through submerged aquatic canopies. Horizontal in-canopy particle image velocimetry (PIV) and wavemaker-measurement synchronization allowed direct volume averaging and ensemble averaging by wave phase, which were used to fully resolve the volume-averaged unsteady momentum budget. Parameterizations for the drag, Reynolds stress, vertical advection, wake production and shear production were tested against the laboratory measurements. The drag was found to have small errors due to unsteadiness and the finite aspect ratio of the canopy elements. The Smagorinsky model for the Reynolds stress showed much better agreement with the measurements than the quadratic friction parameterization used in the literature. A proposed parameterization for the vertical advection based on linear wave theory was also found to be effective and is much more computationally efficient than solving the pressure Poisson equation. A simple 1D 0-equation Reynolds-averaged Navier–Stokes (RANS) model was developed to use these parameterizations. The basic framework of the model is an extrapolation from previous 2- and 3-box models to 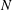 $N$ boxes. While the resolution of the model is flexible, the filter length for the Smagorinsky parameterization has to be chosen appropriately. With the proper filter length, the
$N$ boxes. While the resolution of the model is flexible, the filter length for the Smagorinsky parameterization has to be chosen appropriately. With the proper filter length, the 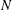 $N$ -box model demonstrated good agreement with the measurements at both low and high resolution. Scaling analysis was used to establish a region of parameter space where the
$N$ -box model demonstrated good agreement with the measurements at both low and high resolution. Scaling analysis was used to establish a region of parameter space where the 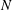 $N$ -box model is expected to be effective. The following conditions define this region: the wave-induced velocity is of similar or greater magnitude than the background current, the drag to shear length ratio is small enough to produce canopy behaviour, the wave orbital excursion is not much larger than the drag length, the Froude number is small and the canopy is under shallow submergence, yet far from emergent. Under these assumptions, the dominant balance is between pressure and unsteadiness, the drag is secondary, and the other terms are small. The simple Reynolds stress parameterization in the
$N$ -box model is expected to be effective. The following conditions define this region: the wave-induced velocity is of similar or greater magnitude than the background current, the drag to shear length ratio is small enough to produce canopy behaviour, the wave orbital excursion is not much larger than the drag length, the Froude number is small and the canopy is under shallow submergence, yet far from emergent. Under these assumptions, the dominant balance is between pressure and unsteadiness, the drag is secondary, and the other terms are small. The simple Reynolds stress parameterization in the 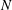 $N$ -box model is appropriate under these conditions because the Reynolds stress is unlikely to be the dominant source of error. This finding is important because the Reynolds stress is typically one of the dominant drivers of computational cost and model complexity. Based on these findings, the
$N$ -box model is appropriate under these conditions because the Reynolds stress is unlikely to be the dominant source of error. This finding is important because the Reynolds stress is typically one of the dominant drivers of computational cost and model complexity. Based on these findings, the 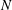 $N$ -box model is expected to be a practical tool for a wide range of combined wave–current canopy flows because of its simplicity and computational efficiency.
$N$ -box model is expected to be a practical tool for a wide range of combined wave–current canopy flows because of its simplicity and computational efficiency.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 29
- Cited by


