Article contents
Shear thickening of a non-colloidal suspension with a viscoelastic matrix
Published online by Cambridge University Press: 18 October 2019
Abstract
We study the rheology of a non-colloidal suspension of rigid spherical particles interacting with a viscoelastic matrix. Three-dimensional numerical simulations under shear flow are performed using the smoothed particle hydrodynamics method and compared with experimental data available in the literature using different constant-viscosity elastic Boger fluids. The rheological properties of the Boger matrices are matched in simulation under viscometric flow conditions. Suspension rheology under dilute to semi-concentrated conditions (i.e. up to solid volume fraction 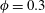 $\unicode[STIX]{x1D719}=0.3$) is explored. It is found that at small Deborah numbers
$\unicode[STIX]{x1D719}=0.3$) is explored. It is found that at small Deborah numbers 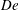 $De$ (based on the macroscopic imposed shear rate), relative suspension viscosities
$De$ (based on the macroscopic imposed shear rate), relative suspension viscosities 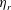 $\unicode[STIX]{x1D702}_{r}$ exhibit a plateau at every concentration investigated. By increasing
$\unicode[STIX]{x1D702}_{r}$ exhibit a plateau at every concentration investigated. By increasing 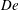 $De$, shear thickening is observed, which is related to the extensional thickening of the underlying viscoelastic matrix. Under dilute conditions (
$De$, shear thickening is observed, which is related to the extensional thickening of the underlying viscoelastic matrix. Under dilute conditions (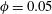 $\unicode[STIX]{x1D719}=0.05$), numerical results for
$\unicode[STIX]{x1D719}=0.05$), numerical results for 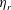 $\unicode[STIX]{x1D702}_{r}$ agree quantitatively with experimental data in both the
$\unicode[STIX]{x1D702}_{r}$ agree quantitatively with experimental data in both the 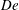 $De$ and
$De$ and 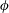 $\unicode[STIX]{x1D719}$ dependences. Even under dilute conditions, simulations of full many-particle systems with no a priori specification of their spatial distribution need to be considered to recover precisely experimental values. By increasing the solid volume fraction towards
$\unicode[STIX]{x1D719}$ dependences. Even under dilute conditions, simulations of full many-particle systems with no a priori specification of their spatial distribution need to be considered to recover precisely experimental values. By increasing the solid volume fraction towards 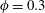 $\unicode[STIX]{x1D719}=0.3$, despite the fact that the trend is well captured, the agreement remains qualitative with discrepancies arising in the absolute values of
$\unicode[STIX]{x1D719}=0.3$, despite the fact that the trend is well captured, the agreement remains qualitative with discrepancies arising in the absolute values of 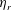 $\unicode[STIX]{x1D702}_{r}$ obtained from simulations and experiments but also with large deviations existing among different experiments. With regard to the specific mechanism of elastic thickening, the microstructural analysis shows that elastic thickening correlates well with the average viscoelastic dissipation function
$\unicode[STIX]{x1D702}_{r}$ obtained from simulations and experiments but also with large deviations existing among different experiments. With regard to the specific mechanism of elastic thickening, the microstructural analysis shows that elastic thickening correlates well with the average viscoelastic dissipation function 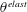 $\unicode[STIX]{x1D703}^{elast}$, requiring a scaling as
$\unicode[STIX]{x1D703}^{elast}$, requiring a scaling as 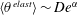 $\langle \unicode[STIX]{x1D703}^{elast}\rangle \sim De^{\unicode[STIX]{x1D6FC}}$ with
$\langle \unicode[STIX]{x1D703}^{elast}\rangle \sim De^{\unicode[STIX]{x1D6FC}}$ with 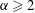 $\unicode[STIX]{x1D6FC}\geqslant 2$ to take place. Locally, despite the fact that regions of large polymer stretching (and viscoelastic dissipation) can occur everywhere in the domain, flow regions uniquely responsible for the elastic thickening are well correlated to areas with significant extensional component.
$\unicode[STIX]{x1D6FC}\geqslant 2$ to take place. Locally, despite the fact that regions of large polymer stretching (and viscoelastic dissipation) can occur everywhere in the domain, flow regions uniquely responsible for the elastic thickening are well correlated to areas with significant extensional component.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 32
- Cited by

