Article contents
Self-preservation in a zero pressure gradient rough-wall turbulent boundary layer
Published online by Cambridge University Press: 22 December 2015
Abstract
A self-preservation (SP) analysis is carried out for a zero pressure gradient (ZPG) rough-wall turbulent boundary layer with a view to establishing the requirements of complete SP (i.e. SP across the entire layer) and determining if these are achievable. The analysis shows that SP is achievable in certain rough-wall boundary layers (irrespectively of the Reynolds number 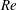 $Re$ ), when the mean viscous stress is zero or negligible compared to the form drag across the entire boundary layer. In this case, the velocity scale
$Re$ ), when the mean viscous stress is zero or negligible compared to the form drag across the entire boundary layer. In this case, the velocity scale 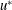 $u^{\ast }$ must be constant, the length scale
$u^{\ast }$ must be constant, the length scale 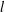 $l$ should vary linearly with the streamwise distance
$l$ should vary linearly with the streamwise distance  $x$ and the roughness height
$x$ and the roughness height 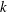 $k$ must be proportional to
$k$ must be proportional to 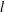 $l$ . Although this result is consistent with that of Rotta (Prog. Aeronaut. Sci., vol. 2 (1), 1962, pp. 1–95), it is derived in a more rigorous manner than the method employed by Rotta. Further, it is noted that complete SP is not possible in a smooth-wall ZPG turbulent boundary layer. The SP conditions are tested against published experimental data on both a smooth wall (Kulandaivelu, 2012, PhD thesis, The University of Melbourne) and a rough wall, where the roughness height increases linearly with
$l$ . Although this result is consistent with that of Rotta (Prog. Aeronaut. Sci., vol. 2 (1), 1962, pp. 1–95), it is derived in a more rigorous manner than the method employed by Rotta. Further, it is noted that complete SP is not possible in a smooth-wall ZPG turbulent boundary layer. The SP conditions are tested against published experimental data on both a smooth wall (Kulandaivelu, 2012, PhD thesis, The University of Melbourne) and a rough wall, where the roughness height increases linearly with  $x$ (Kameda et al., J. Fluid Sci. Technol., vol. 3 (1), 2008, pp. 31–42). Complete SP in a ZPG rough-wall turbulent boundary layer seems indeed possible when
$x$ (Kameda et al., J. Fluid Sci. Technol., vol. 3 (1), 2008, pp. 31–42). Complete SP in a ZPG rough-wall turbulent boundary layer seems indeed possible when 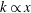 $k\propto x$ .
$k\propto x$ .
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 17
- Cited by


