Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-28T03:17:33.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Sedimentation of finite-size spheres in quiescent and turbulent environments

Published online by Cambridge University Press:  12 January 2016

Walter Fornari ,
Francesco Picano  and
Luca Brandt
Walter Fornari*
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-10044 Stockholm, Sweden
Francesco Picano
Affiliation:
Department of Industrial Engineering, University of Padova, Via Venezia 1, 35131 Padua, Italy
Luca Brandt
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-10044 Stockholm, Sweden
*
†Email address for correspondence: fornari@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Sedimentation of a dispersed solid phase is widely encountered in applications and environmental flows, yet little is known about the behaviour of finite-size particles in homogeneous isotropic turbulence. To fill this gap, we perform direct numerical simulations of sedimentation in quiescent and turbulent environments using an immersed boundary method to account for the dispersed rigid spherical particles. 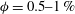The solid volume fractions considered are ${\it\phi}=0.5{-}1\,\%$, while the solid to fluid density ratio 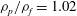${\it\rho}_{p}/{\it\rho}_{f}=1.02$. The particle radius is chosen to be approximately six Kolmogorov length scales. The results show that the mean settling velocity is lower in an already turbulent flow than in a quiescent fluid. The reductions with respect to a single particle in quiescent fluid are approximately 12 % and 14 % for the two volume fractions investigated. The probability density function of the particle velocity is almost Gaussian in a turbulent flow, whereas it displays large positive tails in quiescent fluid. These tails are associated with the intermittent fast sedimentation of particle pairs in drafting–kissing–tumbling motions. The particle lateral dispersion is higher in a turbulent flow, whereas the vertical one is, surprisingly, of comparable magnitude as a consequence of the highly intermittent behaviour observed in the quiescent fluid. Using the concept of mean relative velocity we estimate the mean drag coefficient from empirical formulae and show that non-stationary effects, related to vortex shedding, explain the increased reduction in mean settling velocity in a turbulent environment.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 640 - 669
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52 (02), 245–268.Google Scholar
Bec, J., Homann, H. & Ray, S. S. 2014 Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112 (18), 184501.Google Scholar
Bellani, G. & Variano, E. A. 2012 Slip velocity of large neutrally buoyant particles in turbulent flows. New J. Phys. 14 (12), 125009.Google Scholar
Bergougnoux, L., Bouchet, G., Lopez, D. & Guazzelli, E. 2014 The motion of solid spherical particles falling in a cellular flow field at low Stokes number. Phys. Fluids 26 (9), 093302.Google Scholar
Bosse, T., Kleiser, L. & Meiburg, E. 2006 Small particles in homogeneous turbulence: settling velocity enhancement by two-way coupling. Phys. Fluids 18 (2), 027102.Google Scholar
Bouchet, G., Mebarek, M. & Dušek, J. 2006 Hydrodynamic forces acting on a rigid fixed sphere in early transitional regimes. Eur. J. Mech. (B/Fluids) 25 (3), 321–336.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3), 242–251.Google Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.Google Scholar
Bush, J. W. M., Thurber, B. A. & Blanchette, F. 2003 Particle clouds in homogeneous and stratified environments. J. Fluid Mech. 489, 29–54.Google Scholar
Byron, M. L.2015 The rotation and translation of non-spherical particles in homogeneous isotropic turbulence, arXiv:1506.00478.Google Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–203.CrossRefGoogle Scholar
Cisse, M., Homann, H. & Bec, J. 2013 Slipping motion of large neutrally buoyant particles in turbulence. J. Fluid Mech. 735, R1.Google Scholar
Climent, E. & Maxey, M. R. 2003 Numerical simulations of random suspensions at finite Reynolds numbers. Intl. J. Multiphase Flow 29 (4), 579–601.Google Scholar
Corrsin, S. E. & Lumley, J. 1956 On the equation of motion for a particle in turbulent fluid. Appl. Sci. Res. 6 (2), 114–116.CrossRefGoogle Scholar
Csanady, G. T. 1963 Turbulent diffusion of heavy particles in the atmosphere. J. Atmos. Sci. 20 (3), 201–208.2.0.CO;2>CrossRefGoogle Scholar
Di Felice, R. 1999 The sedimentation velocity of dilute suspensions of nearly monosized spheres. Intl. J. Multiphase Flow 25 (4), 559–574.CrossRefGoogle Scholar
Doostmohammadi, A. & Ardekani, A. M. 2015 Suspension of solid particles in a density stratified fluid. Phys. Fluids 27 (2), 023302.Google Scholar
Elgobashi, S. 1991 Particle-laden turbulent flows: direct simulation and closure models. Appl. Sci. Res. 48 (3–4), 301–314.CrossRefGoogle Scholar
Fortes, A. F., Joseph, D. D. & Lundgren, T. S. 1987 Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 177, 467–483.Google Scholar
Garcia-Villalba, M., Kidanemariam, A. G. & Uhlmann, M. 2012 DNS of vertical plane channel flow with finite-size particles: Voronoi analysis, acceleration statistics and particle-conditioned averaging. Intl. J. Multiphase Flow 46, 54–74.CrossRefGoogle Scholar
Garside, J. & Al-Dibouni, M. R. 1977 Velocity-voidage relationships for fluidization and sedimentation in solid–liquid systems. Ind. Eng. Chem. Process Des. Develop. 16 (2), 206–214.CrossRefGoogle Scholar
Good, G. H., Ireland, P. J., Bewley, G. P., Bodenschatz, E., Collins, L. R. & Warhaft, Z. 2014 Settling regimes of inertial particles in isotropic turbulence. J. Fluid Mech. 759, R3.Google Scholar
Guazzelli, E. & Morris, J. F. 2012 A Physical Introduction to Suspension Dynamics, Cambridge University Press.Google Scholar
Gustavsson, K., Vajedi, S. & Mehlig, B. 2014 Clustering of particles falling in a turbulent flow. Phys. Rev. Lett. 112 (21), 214501.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (02), 317–328.Google Scholar
Homann, H., Bec, J. & Grauer, R. 2013 Effect of turbulent fluctuations on the drag and lift forces on a towed sphere and its boundary layer. J. Fluid Mech. 721, 155–179.Google Scholar
Hwang, W. & Eaton, J. K. 2006 Homogeneous and isotropic turbulence modulation by small heavy ( $St\sim 50$ ) particles. J. Fluid Mech. 564, 361–393.Google Scholar
Johnson, A. A. & Tezduyar, T. E. 1996 Simulation of multiple spheres falling in a liquid-filled tube. Comput. Meth. Appl. Mech. Engng 134 (3), 351–373.Google Scholar
Kempe, T. & Fröhlich, J. 2012 An improved immersed boundary method with direct forcing for the simulation of particle laden flows. J. Comput. Phys. 231 (9), 3663–3684.Google Scholar
Ladd, A. J. C. 1993 Dynamical simulations of sedimenting spheres. Phys. Fluids A 5 (2), 299–310.Google Scholar
Ladd, A. J. C. & Verberg, R. 2001 Lattice-Boltzmann simulations of particle–fluid suspensions. J. Stat. Phys. 104 (5–6), 1191–1251.CrossRefGoogle Scholar
Lambert, R. A., Picano, F., Breugem, W.-P. & Brandt, L. 2013 Active suspensions in thin films: nutrient uptake and swimmer motion. J. Fluid Mech. 733, 528–557.Google Scholar
Lashgari, I., Picano, F., Breugem, W.-P. & Brandt, L. 2014 Laminar, turbulent, and inertial shear-thickening regimes in channel flow of neutrally buoyant particle suspensions. Phys. Rev. Lett. 113 (25), 254502.Google Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Merle, A., Legendre, D. & Magnaudet, J. 2005 Forces on a high-Reynolds-number spherical bubble in a turbulent flow. J. Fluid Mech. 532, 53–62.CrossRefGoogle Scholar
Mordant, N. & Pinton, J.-F. 2000 Velocity measurement of a settling sphere. Eur. Phys. J. B 18 (2), 343–352.Google Scholar
Olivieri, S., Picano, F., Sardina, G., Iudicone, D. & Brandt, L. 2014 The effect of the Basset history force on particle clustering in homogeneous and isotropic turbulence. Phys. Fluids 26 (4), 041704.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.Google Scholar
Pignatel, F., Nicolas, M. & Guazzelli, E. 2011 A falling cloud of particles at a small but finite Reynolds number. J. Fluid Mech. 671, 34–51.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prosperetti, A. 2015 Life and death by boundary conditions. J. Fluid Mech. 768, 1–4.Google Scholar
Richardson, J. F. & Zaki, W. N. 1954 The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Engng Sci. 3 (2), 65–73.Google Scholar
Sangani, A. S. & Acrivos, A. 1982 Slow flow past periodic arrays of cylinders with application to heat transfer. Intl. J. Multiphase Flow 8 (3), 193–206.Google Scholar
Siewert, C., Kunnen, R. P. J. & Schröder, W. 2014 Collision rates of small ellipsoids settling in turbulence. J. Fluid Mech. 758, 686–701.Google Scholar
Sobral, Y. D., Oliveira, T. F. & Cunha, F. R. 2007 On the unsteady forces during the motion of a sedimenting particle. Powder Technol. 178 (2), 129–141.Google Scholar
Stout, J. E., Arya, S. P. & Genikhovich, E. L. 1995 The effect of nonlinear drag on the motion and settling velocity of heavy particles. J. Atmos. Sci. 52 (22), 3836–3848.Google Scholar
Sugiyama, K., Calzavarini, E. & Lohse, D. 2008 Microbubbly drag reduction in Taylor–Couette flow in the wavy vortex regime. J. Fluid Mech. 608, 21–41.Google Scholar
Tchen, C.-M.1947 Mean value and correlation problems connected with the motion of small particles suspended in a turbulent fluid. PhD thesis, TU Delft, Delft University of Technology.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Tunstall, E. B. & Houghton, G. 1968 Retardation of falling spheres by hydrodynamic oscillations. Chem. Engng Sci. 23 (9), 1067–1081.CrossRefGoogle Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.Google Scholar
Vincent, A. & Meneguzzi, M. 1991 The satial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.Google Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Yin, X. & Koch, D. L. 2007 Hindered settling velocity and microstructure in suspensions of solid spheres with moderate Reynolds numbers. Phys. Fluids 19 (9), 093302.Google Scholar
Zhan, C., Sardina, G., Lushi, E. & Brandt, L. 2014 Accumulation of motile elongated micro-organisms in turbulence. J. Fluid Mech. 739, 22–36.Google Scholar
Zhang, Q. & Prosperetti, A. 2010 Physics-based analysis of the hydrodynamic stress in a fluid–particle system. Phys. Fluids 22 (3), 033306.Google Scholar