Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-05T04:58:42.030Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling of second- and higher-order structure functions in turbulent boundary layers

Published online by Cambridge University Press:  30 March 2015

C. M. de Silva ,
I. Marusic ,
J. D. Woodcock  and
C. Meneveau
C. M. de Silva*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Australia
I. Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Australia
J. D. Woodcock
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Australia
C. Meneveau
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA
*
†Email address for correspondence: desilvac@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

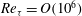The statistical properties of wall turbulence in the logarithmic region are investigated using structure functions of the streamwise velocity. To this end, datasets that span several orders of magnitude of Reynolds numbers are used, up to $Re_{{\it\tau}}=O(10^{6})$, providing uniquely large scale separations for scrutinising previously proposed scaling laws. 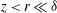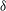For the second-order structure functions strong support is found simultaneously for power-law scalings in the Kolmogorov inertial subrange and for logarithmic scaling at larger scales within the inertial range ($z<r\ll {\it\delta}$, where $z$ is the distance from the wall, $r$ the scale, and ${\it\delta}$ the boundary layer thickness). The observed scalings are shown to agree between the datasets, which include both temporal and spatial velocity signals and span from laboratory to atmospheric flows, showing a degree of universality in the results presented. An examination of higher even-order structure functions also shows support for logarithmic scaling behaviour for 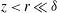$z<r\ll {\it\delta}$, provided that the Reynolds number is sufficiently high. These findings are interpreted by generalising the work of Meneveau & Marusic (J. Fluid Mech., vol. 719, 2013) and introducing bridging relations between higher-order moments of velocity fluctuations and structure functions. Further, a physical model based on the attached-eddy hypothesis is utilised to derive various properties of the structure functions for the energy-containing scales of the logarithmic region. The descriptions derived from the model are shown to be supported by the experimental data.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , pp. 654 - 686
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anselmet, F., Gagne, Yl., Hopfinger, E. J. & Antonia, R. A. 1984 High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 140 (63), 63–89.Google Scholar
Arad, I., Biferale, L., Mazzitelli, I. & Procaccia, I. 1999 Disentangling scaling properties in anisotropic and inhomogeneous turbulence. Phys. Rev. Lett. 82 (25), 5040–5043.Google Scholar
Atkinson, C., Buchmann, N. A., Amili, O. & Soria, J. 2013 Appropriate spatial filtering of 2D and 3D PIV measurements of wall-bounded turbulent flows. In PIV 13; 10th International Symposium on Particle Image Velocimetry, Delft, The Netherlands, July 1–3, 2013, Delft University of Technology, Faculty of Mechanical, Maritime and Materials Engineering, and Faculty of Aerospace Engineering.Google Scholar
Atkinson, C., Buchmann, N. A. & Soria, J. 2014 An experimental investigation of turbulent convection velocities in a turbulent boundary layer. Flow Turbul. Combust. 94, 1–17.Google Scholar
Benzi, R., Amati, G., Casciola, C. M., Toschi, F. & Piva, R. 1999 Intermittency and scaling laws for wall bounded turbulence. Phys. Fluids 11 (6), 1284–1286.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to $Re_{{\it\tau}}\approx 4000$ . J. Fluid Mech. 742, 171–191.Google Scholar
Casciola, C. M., Gualtieri, P., Benzi, R. & Piva, R. 2003 Scale-by-scale budget and similarity laws for shear turbulence. J. Fluid Mech. 476, 105–114.Google Scholar
Casciola, C. M., Gualtieri, P., Jacob, B. & Piva, R. 2005 Scaling properties in the production range of shear dominated flows. Phys. Rev. Lett. 95 (2), 024503.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Coles, D.1962 The turbulent boundary layer in a compressible fluid, Tech. Rep. R-403-PR. The RAND Corporation.Google Scholar
Davidson, P. A. & Krogstad, P. Å. 2009 A simple model for the streamwise fluctuations in the log-law region of a boundary layer. Phys. Fluids 21 (5), 055105.Google Scholar
Davidson, P. A. & Krogstad, P. Å. 2014 A universal scaling for low-order structure functions in the log-law region of smooth- and rough-wall boundary layers. J. Fluid Mech. 752, 140–156.Google Scholar
Davidson, P. A., Krogstad, P. A. & Nickels, T. B. 2006a A refined interpretation of the logarithmic structure function law in wall layer turbulence. Phys. Fluids 18 (6).Google Scholar
Davidson, P. A., Nickels, T. B. & Krogstad, P.-Å. 2006b The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.CrossRefGoogle Scholar
Del Alamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Frisch, U. 1995 Turbulence: the Legacy of AN Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Gualtieri, P., Casciola, C. M., Benzi, R., Amati, G. & Piva, R. 2002 Scaling laws and intermittency in homogeneous shear flow. Phys. Fluids 14 (2), 583–596.CrossRefGoogle Scholar
Hinze, J. O. 1975 Turbulence, 2nd edn. McGraw-Hill.Google Scholar
Högström, U., Hunt, J. C. R. & Smedman, A.-S. 2002 Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Boundary-Layer Meteorol. 103, 101–124.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{{\it\tau}}=2003$ . Phys. Fluids 18, 011702.Google Scholar
Hultmark, M. 2012 A theory for the streamwise turbulent fluctuations in high Reynolds number pipe flow. J. Fluid Mech. 707, 575–584.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Jacob, B., Biferale, L., Iuso, G. & Casciola, C. M. 2004 Anisotropic fluctuations in turbulent shear flows. Phys. Fluids 16 (11), 4135–4142.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kolmogorov, A. N. 1941 Finite size corrections to scaling in high Reynolds number turbulence. C. R. Acad. Sci. URSS 30, 301–305.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high Reynolds number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Kurien, S., Lvov, V. S., Procaccia, I. & Sreenivasan, K. R. 2000 Scaling structure of the velocity statistics in atmospheric boundary layers. Phys. Rev. E 61 (1), 407.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_{{\it\tau}}=5200$ . J. Fluid Mech. (under review), http://arxiv.org/abs/1410.7809.Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13, 735.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
McKeon, B. J. & Morrison, J. F. 2007 Asymptotic scaling in turbulent pipe flow. Phil. Trans. R. Soc. Lond. A 365 (1852), 771–787.Google ScholarPubMed
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1–R11.Google Scholar
Meneveau, C. & Sreenivasan, K. R. 1987 Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 59 (13), 1424.Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.Google Scholar
Nelkin, M. 1990 Multifractal scaling of velocity derivatives in turbulence. Phys. Rev. A 42 (12), 7226–7229.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the $k_{1}^{-1}$ law in a high Reynolds number turbulent boundary layer. Phy. Rev. Lett. 95 (7), 074501.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119 (173), 106–121.Google Scholar
Perry, A. E., Henbest, S. M. & Chong, M. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Perry, A. E. & Li, J. Ds. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.CrossRefGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Pirozzoli, S. & Bernardini, M. 2013 Probing high-Reynolds-number effects in numerical boundary layers. Phys. Fluids 25, 021704.Google Scholar
Poggi, D., Porporato, A. & Ridolfi, L. 2003 Analysis of the small-scale structure of turbulence on smooth and rough walls. Phys. Fluids 15 (1), 35–46.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Saikrishnan, N., De Angelis, E., Longmire, E. K., Marusic, I., Casciola, C. M. & Piva, R. 2012 Reynolds number effects on scale energy balance in wall turbulence. Phys. Fluids 24 (1), 015101.CrossRefGoogle Scholar
Schultz, M. P. & Flack, K. A. 2005 Outer layer similarity in fully rough turbulent boundary layers. Exp. Fluids 38 (3), 328–340.Google Scholar
She, Z. S. & Leveque, E. 1994 Universal scaling law in fully developed turbulence. Phys. Rev. Lett. 72, 1424.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to ${\it\delta}^{+}=2000$ . Phys. Fluids 25 (10), 105102.Google Scholar
de Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014 High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26 (2), 025117.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Stevens, R., Wilczek, M. & Meneveau, C. 2014 Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow. J. Fluid Mech. 757, 888–907.CrossRefGoogle Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Toschi, F., Amati, G., Succi, S., Benzi, R. & Piva, R. 1999 Intermittency and structure functions in channel flow turbulence. Phys. Rev. Lett. 82 (25), 5044–5047.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 015104.Google Scholar
Zhao, R. & Smits, A. J. 2007 Scaling of the wall-normal turbulence component in high Reynolds number pipe flow. J. Fluid Mech. 576, 457–473.Google Scholar