Article contents
Scales and self-sustained mechanism of reattachment unsteadiness in separated shock wave/boundary layer interaction
Published online by Cambridge University Press: 04 November 2024
Abstract
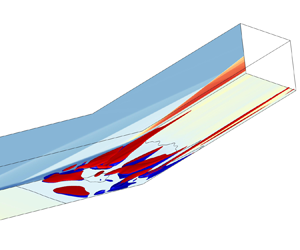
The spatio-temporal scales, as well as a comprehensive self-sustained mechanism of the reattachment unsteadiness in shock wave/boundary layer interaction, are investigated in this study. Direct numerical simulations reveal that the reattachment unsteadiness of a Mach 7.7 laminar inflow causes over  $26\,\%$ variation in wall friction and up to
$26\,\%$ variation in wall friction and up to  $20\,\%$ fluctuation in heat flux at the reattachment of the separation bubble. A statistical approach, based on the local reattachment upstream movement, is proposed to identify the spanwise and temporal scales of reattachment unsteadiness. It is found that two different types, i.e. self-induced and random processes, dominate different regions of reattachment. A self-sustained mechanism is proposed to comprehend the reattachment unsteadiness in the self-induced region. The intrinsic instability of the separation bubble transports vorticity downstream, resulting in an inhomogeneous reattachment line, which gives rise to baroclinic production of quasi-streamwise vortices. The pairing of these vortices initiates high-speed streaks and shifts the reattachment line upstream. Ultimately, viscosity dissipates the vortices, triggering instability and a new cycle of reattachment unsteadiness. The temporal scale and maximum vorticity are estimated with the self-sustained mechanism via order-of-magnitude analysis of the enstrophy. The advection speed of friction, derived from the assumption of coherent structures advecting with a Blasius-type boundary layer, aligns with the numerical findings.
$20\,\%$ fluctuation in heat flux at the reattachment of the separation bubble. A statistical approach, based on the local reattachment upstream movement, is proposed to identify the spanwise and temporal scales of reattachment unsteadiness. It is found that two different types, i.e. self-induced and random processes, dominate different regions of reattachment. A self-sustained mechanism is proposed to comprehend the reattachment unsteadiness in the self-induced region. The intrinsic instability of the separation bubble transports vorticity downstream, resulting in an inhomogeneous reattachment line, which gives rise to baroclinic production of quasi-streamwise vortices. The pairing of these vortices initiates high-speed streaks and shifts the reattachment line upstream. Ultimately, viscosity dissipates the vortices, triggering instability and a new cycle of reattachment unsteadiness. The temporal scale and maximum vorticity are estimated with the self-sustained mechanism via order-of-magnitude analysis of the enstrophy. The advection speed of friction, derived from the assumption of coherent structures advecting with a Blasius-type boundary layer, aligns with the numerical findings.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by


