Article contents
Roughness receptivity and shielding in a flat plate boundary layer
Published online by Cambridge University Press: 20 July 2015
Abstract
Surface roughness can affect boundary layer transition by acting as a receptivity mechanism for transient growth. While experiments have investigated transient growth of steady disturbances generated by discrete roughness elements, very few have studied distributed surface roughness. Some work predicts a‘shielding’ effect, where smaller distributed roughness displaces the boundary layer away from the wall and lessens the impact of larger roughness peaks. This work describes an experiment specifically designed to study this effect. Three roughness configurations (a deterministic distributed roughness patch, a slanted rectangular prism, and the combination of the two) were manufactured using rapid prototyping and installed flush with the wall of a flat plate boundary layer. Naphthalene flow visualization and hotwire anemometry were used to characterize the boundary layer in the wakes of the different roughness configurations. Distributed roughness with roughness Reynolds numbers ( 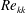 $\mathit{Re}_{kk}$ ) between 113 and 182 initiated small-amplitude disturbances that underwent transient growth. The discrete roughness element created a pair of high- and low-speed steady streaks in the boundary layer at a sub-critical Reynolds number (
$\mathit{Re}_{kk}$ ) between 113 and 182 initiated small-amplitude disturbances that underwent transient growth. The discrete roughness element created a pair of high- and low-speed steady streaks in the boundary layer at a sub-critical Reynolds number ( 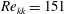 $\mathit{Re}_{kk}=151$ ). At a higher Reynolds number (
$\mathit{Re}_{kk}=151$ ). At a higher Reynolds number ( 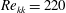 $\mathit{Re}_{kk}=220$ ), the discrete element created a turbulent wedge 15 boundary layer thicknesses downstream. When the distributed roughness was added around the discrete roughness, the discrete element’s wake amplitude was decreased. For the higher Reynolds number, this provided a small but measurable transition delay. The distributed roughness redirects energy from longer spanwise wavelength modes to shorter spanwise wavelength modes. The presence of the distributed roughness also decreased the growth rate of secondary instabilities in the roughness wake. This work demonstrates that shielding can delay roughness-induced transition and lays the ground work for future studies of roughness-induced transition.
$\mathit{Re}_{kk}=220$ ), the discrete element created a turbulent wedge 15 boundary layer thicknesses downstream. When the distributed roughness was added around the discrete roughness, the discrete element’s wake amplitude was decreased. For the higher Reynolds number, this provided a small but measurable transition delay. The distributed roughness redirects energy from longer spanwise wavelength modes to shorter spanwise wavelength modes. The presence of the distributed roughness also decreased the growth rate of secondary instabilities in the roughness wake. This work demonstrates that shielding can delay roughness-induced transition and lays the ground work for future studies of roughness-induced transition.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 31
- Cited by


