Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ping, Huan
Zhu, Hongbo
Zhang, Kai
Zhou, Dai
Bao, Yan
and
Han, Zhaolong
2021.
Vortex-induced vibrations of two rigidly coupled circular cylinders of unequal diameters at low Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 10,
Carvalho, I.A.
and
Assi, G.R.S.
2022.
Enhanced control of the turbulent flow past a circular cylinder with rotating rods inspired by an inviscid solution.
Journal of Fluids and Structures,
Vol. 113,
Issue. ,
p.
103652.
Biswas, Neelakash
Cicolin, Murilo M.
and
Buxton, Oliver R.H.
2022.
Energy exchanges in the flow past a cylinder with a leeward control rod.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Alziadeh, M.
and
Mohany, A.
2022.
Vortex shedding characteristics and aerodynamic forces of a finned cylinder in cross-flow.
Physics of Fluids,
Vol. 34,
Issue. 9,
Steiros, K.
Bempedelis, N.
and
Cicolin, M.M.
2022.
An analytical blockage correction model for high-solidity turbines.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Gu, Honglu
Guo, Haiyan
Li, Xiaomin
and
Li, Fuheng
2023.
Experimental investigation into the effect of diameter ratio on the flow-induced vibration of tandem flexible cylinders.
Ocean Engineering,
Vol. 288,
Issue. ,
p.
115978.
Bai, Honglei
Wang, Fei
Zhang, Shixiong
Zhang, Weiguo
and
Lin, Yufeng
2023.
Square cylinder flow controlled by a synthetic jet at one leading edge.
Physics of Fluids,
Vol. 35,
Issue. 3,
Hao, Yanming
Lee, Cunbiao
and
Cai, Qingdong
2023.
The dynamic feedback cycle of the two-dimensional Kármán vortex street.
Physics of Fluids,
Vol. 35,
Issue. 2,
Cicolin, M.M.
Bearman, P.W.
Assi, G.R.S.
and
Buxton, O.R.H.
2023.
Bistability in the wake of a circular cylinder with passive control using two leeward rods.
Journal of Fluids and Structures,
Vol. 120,
Issue. ,
p.
103918.
Zhao, Ming
2023.
A review of recent studies on the control of vortex-induced vibration of circular cylinders.
Ocean Engineering,
Vol. 285,
Issue. ,
p.
115389.
Hammad, Omar S.
and
Mohany, Atef
2023.
Vortex shedding characteristics and hydrodynamic forces of stationary and elastically mounted side-by-side cylinders fitted with small diameter control rods.
Journal of Fluids and Structures,
Vol. 120,
Issue. ,
p.
103908.
Alziadeh, M.
and
Mohany, A.
2023.
Flow structure and aerodynamic forces of finned cylinders during flow-induced acoustic resonance.
Journal of Fluids and Structures,
Vol. 119,
Issue. ,
p.
103887.
G. de Oliveira, Francisco J.
Khodaei, Zahra Sharif
and
Buxton, Oliver R. H.
2024.
Simultaneous measurement of the distributed longitudinal strain and velocity field for a cantilevered cylinder exposed to turbulent cross flow.
Experiments in Fluids,
Vol. 65,
Issue. 9,
Noufal, R.
Alziadeh, M.
and
Mohany, A.
2024.
Control of vortex shedding and acoustic resonance of a circular cylinder in cross-flow.
Journal of Fluids and Structures,
Vol. 126,
Issue. ,
p.
104094.
Carvalho, I.A.
and
Assi, G.R.S.
2024.
On the omnidirectionality of a system with eight spinning rods for wake control of a circular cylinder in laminar regime.
Journal of Fluids and Structures,
Vol. 124,
Issue. ,
p.
104053.
Silva, Paulo H.N.
and
Assi, Gustavo R.S.
2024.
Experimental investigation on the optimal control of vortex shedding of a circular cylinder with rotating rods at moderate Reynolds numbers.
Journal of Fluids and Structures,
Vol. 124,
Issue. ,
p.
104026.
Carvalho, I.A.
and
Assi, G.R.S.
2024.
Omnidirectional control of the wake of a circular cylinder with spinning rods subject to a turbulent flow.
Journal of Fluids and Structures,
Vol. 130,
Issue. ,
p.
104191.
Gong, Jiarui
Wang, Jiansheng
Liu, Xueling
and
Jiang, Haoran
2024.
Numerical comprehensive evaluation of the flow control effect on a circular cylinder with a control rod.
Fluid Dynamics Research,
Vol. 56,
Issue. 4,
p.
045502.
Biswas, N.
and
Buxton, O. R. H.
2024.
Progress in Turbulence X.
Vol. 404,
Issue. ,
p.
21.
Zhu, Jing
Wang, Hanfeng
and
Zeng, Lingwei
2024.
Control of the flow around a finite-height square cylinder with slot blowing near its free-end side edges.
Physics of Fluids,
Vol. 36,
Issue. 2,
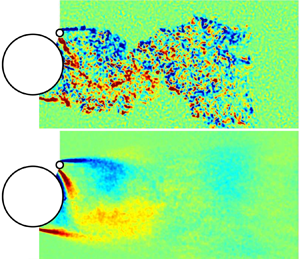
 $D$ (where
$D$ (where  $D$ is the main cylinder diameter). The adjustable parameter was the angular position of the rod,
$D$ is the main cylinder diameter). The adjustable parameter was the angular position of the rod,  $\theta$, which was varied between
$\theta$, which was varied between  $90^{\circ }$ and
$90^{\circ }$ and  $180^{\circ }$ from the front stagnation line. Lift and drag forces were measured separately for the main cylinder and the control rod. A new method for identifying flow states is introduced using PIV to interrogate the instantaneous flow velocity in the gap between the main cylinder and the control rod. Similarly to previous studies, three stable flow states were observed together with a bistable state. The bistable state is very sensitive to the control rod angle with a small change of
$180^{\circ }$ from the front stagnation line. Lift and drag forces were measured separately for the main cylinder and the control rod. A new method for identifying flow states is introduced using PIV to interrogate the instantaneous flow velocity in the gap between the main cylinder and the control rod. Similarly to previous studies, three stable flow states were observed together with a bistable state. The bistable state is very sensitive to the control rod angle with a small change of  ${\pm }1^{\circ }$ being sufficient to change the flow state.
${\pm }1^{\circ }$ being sufficient to change the flow state.

