Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Seis, Christian
2013.
Laminar Boundary Layers in Convective Heat Transport.
Communications in Mathematical Physics,
Vol. 324,
Issue. 3,
p.
995.
Wang, Xiaoming
and
Whitehead, Jared P.
2013.
A bound on the vertical transport of heat in the ‘ultimate’ state of slippery convection at large Prandtl numbers.
Journal of Fluid Mechanics,
Vol. 729,
Issue. ,
p.
103.
Goluskin, David
Johnston, Hans
Flierl, Glenn R.
and
Spiegel, Edward A.
2014.
Convectively driven shear and decreased heat flux.
Journal of Fluid Mechanics,
Vol. 759,
Issue. ,
p.
360.
Whitehead, Jared P.
and
Wittenberg, Ralf W.
2014.
A rigorous bound on the vertical transport of heat in Rayleigh-Bénard convection at infinite Prandtl number with mixed thermal boundary conditions.
Journal of Mathematical Physics,
Vol. 55,
Issue. 9,
Hassanzadeh, Pedram
Chini, Gregory P.
and
Doering, Charles R.
2014.
Wall to wall optimal transport.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
627.
Wen, Baole
Chini, Gregory P.
Kerswell, Rich R.
and
Doering, Charles R.
2015.
Time-stepping approach for solving upper-bound problems: Application to two-dimensional Rayleigh-Bénard convection.
Physical Review E,
Vol. 92,
Issue. 4,
Grooms, Ian
and
Whitehead, Jared P
2015.
Bounds on heat transport in rapidly rotating Rayleigh–Bénard convection.
Nonlinearity,
Vol. 28,
Issue. 1,
p.
29.
Goluskin, David
and
Doering, Charles R.
2016.
Bounds for convection between rough boundaries.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
370.
Goluskin, David
2016.
Internally Heated Convection and Rayleigh-Bénard Convection.
p.
27.
Tilgner, A.
2017.
Bounds on poloidal kinetic energy in plane layer convection.
Physical Review Fluids,
Vol. 2,
Issue. 12,
Motoki, Shingo
Kawahara, Genta
and
Shimizu, Masaki
2018.
Optimal heat transfer enhancement in plane Couette flow.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
1157.
Fantuzzi, Giovanni
2018.
Bounds for Rayleigh–Bénard convection between free-slip boundaries with an imposed heat flux.
Journal of Fluid Mechanics,
Vol. 837,
Issue. ,
Motoki, Shingo
Kawahara, Genta
and
Shimizu, Masaki
2018.
Maximal heat transfer between two parallel plates.
Journal of Fluid Mechanics,
Vol. 851,
Issue. ,
Fantuzzi, Giovanni
Pershin, Anton
and
Wynn, Andrew
2018.
Bounds on heat transfer for Bénard–Marangoni convection at infinite Prandtl number.
Journal of Fluid Mechanics,
Vol. 837,
Issue. ,
p.
562.
Gie, G.-M.
and
Whitehead, J. P.
2019.
Boundary Layer Analysis for Navier-Slip Rayleigh–Bénard Convection: The Non-existence of an Ultimate State.
Journal of Mathematical Fluid Mechanics,
Vol. 21,
Issue. 1,
Farhat, A.
Glatt-Holtz, N. E.
Martinez, V. R.
McQuarrie, S. A.
and
Whitehead, J. P.
2020.
Data Assimilation in Large Prandtl Rayleigh--Bénard Convection from Thermal Measurements.
SIAM Journal on Applied Dynamical Systems,
Vol. 19,
Issue. 1,
p.
510.
Eckhardt, Bruno
Doering, Charles R.
and
Whitehead, Jared P.
2020.
Exact relations between Rayleigh–Bénard and rotating plane Couette flow in two dimensions.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Tilgner, A.
2021.
A rigorous bound on the scaling of dissipation with velocity amplitude in flow past a sphere.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Arslan, Ali
Fantuzzi, Giovanni
Craske, John
and
Wynn, Andrew
2021.
Bounds on heat transport for convection driven by internal heating.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Drivas, Theodore D.
Nguyen, Huy Q.
and
Nobili, Camilla
2022.
Bounds on heat flux for Rayleigh–Bénard convection between Navier-slip fixed-temperature boundaries.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2225,

 ), the Nusselt number (
), the Nusselt number (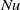 ) is bounded according to
) is bounded according to 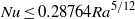 where
where 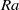 is the standard Rayleigh number. For convection driven by a uniform steady internal heat source between isothermal boundaries, the spatially and temporally averaged (non-dimensional) temperature is bounded from below by
is the standard Rayleigh number. For convection driven by a uniform steady internal heat source between isothermal boundaries, the spatially and temporally averaged (non-dimensional) temperature is bounded from below by 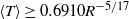 in three dimensions at infinite
in three dimensions at infinite 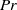 and by
and by 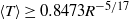 in two dimensions at arbitrary
in two dimensions at arbitrary 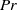 , where
, where 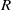 is the heat Rayleigh number proportional to the injected flux.
is the heat Rayleigh number proportional to the injected flux.