Article contents
The rhythm of fountains: the length and time scales of rise height fluctuations at low and high Froude numbers
Published online by Cambridge University Press: 01 July 2013
Abstract
The magnitude and frequency of vertical fluctuations of the top of an axisymmetric miscible Boussinesq fountain forms the focus of this work. We present measurements of these quantities for saline-aqueous fountains in uniform quiescent surroundings. Our results span source Froude numbers 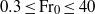 $0. 3\leq {\mathrm{Fr} }_{0} \leq 40$ and, thereby, encompass very weak, weak, intermediate and forced classes of fountain. We identify distinct scalings, based on known quantities at the fountain source, for the frequency of fountain height fluctuations which collapse our data within bands of
$0. 3\leq {\mathrm{Fr} }_{0} \leq 40$ and, thereby, encompass very weak, weak, intermediate and forced classes of fountain. We identify distinct scalings, based on known quantities at the fountain source, for the frequency of fountain height fluctuations which collapse our data within bands of 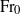 ${\mathrm{Fr} }_{0} $ . Notably, our scalings reveal that the (dimensionless) frequency takes a constant value within each band. These results highlight characteristic time scales for the fluctuations which we decompose into a single, physically apparent, length scale and velocity scale within each band. Moreover, within one particular band, spanning source Froude numbers towards the lower end of the full range considered, we identify unexpectedly long-period fluctuations indicating a near balance of inertia and (opposing) buoyancy at the source. Our analysis identifies four distinct classes of fluctuation behaviour (four bands of
${\mathrm{Fr} }_{0} $ . Notably, our scalings reveal that the (dimensionless) frequency takes a constant value within each band. These results highlight characteristic time scales for the fluctuations which we decompose into a single, physically apparent, length scale and velocity scale within each band. Moreover, within one particular band, spanning source Froude numbers towards the lower end of the full range considered, we identify unexpectedly long-period fluctuations indicating a near balance of inertia and (opposing) buoyancy at the source. Our analysis identifies four distinct classes of fluctuation behaviour (four bands of  ${\mathrm{Fr} }_{0} $ ) and this classification matches well with existing classifications of fountains based on rise heights. As such, we show that an analysis of the behaviour of the fountain top alone, rather than the entire fountain, provides an alternative approach to classifying fountains. The similarity of classifications based on the two different methods confirms that the boundaries between classes mark tangible changes in the physics of fountains. For high
${\mathrm{Fr} }_{0} $ ) and this classification matches well with existing classifications of fountains based on rise heights. As such, we show that an analysis of the behaviour of the fountain top alone, rather than the entire fountain, provides an alternative approach to classifying fountains. The similarity of classifications based on the two different methods confirms that the boundaries between classes mark tangible changes in the physics of fountains. For high 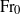 ${\mathrm{Fr} }_{0} $ we show that the dominant fluctuations occur at the scale of the largest eddies which can be contained within the fountain near its top. Extending this, we develop a Strouhal number,
${\mathrm{Fr} }_{0} $ we show that the dominant fluctuations occur at the scale of the largest eddies which can be contained within the fountain near its top. Extending this, we develop a Strouhal number, 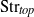 ${\mathrm{Str} }_{top} $ , based on experimental measures of the fountain top, defined such that
${\mathrm{Str} }_{top} $ , based on experimental measures of the fountain top, defined such that  ${\mathrm{Str} }_{top} = 1$ would suggest the dominant fluctuations are caused by a continual cycle of eddies forming and collapsing at this largest physical scale. For high-
${\mathrm{Str} }_{top} = 1$ would suggest the dominant fluctuations are caused by a continual cycle of eddies forming and collapsing at this largest physical scale. For high- 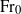 ${\mathrm{Fr} }_{0} $ fountains we find
${\mathrm{Fr} }_{0} $ fountains we find 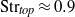 ${\mathrm{Str} }_{top} \approx 0. 9$ .
${\mathrm{Str} }_{top} \approx 0. 9$ .
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 39
- Cited by

