Article contents
Rheology of a suspension of conducting particles in a magnetic field
Published online by Cambridge University Press: 17 May 2019
Abstract
When a suspension of conducting particles is sheared in a magnetic field, the fluid vorticity causes particle rotation. Eddy currents are induced in a conductor rotating in a magnetic field, resulting in magnetic moment, and a magnetic torque due to the external field. In the absence of inertia, the angular velocity of a particle is determined from the condition that the sum of the hydrodynamic and magnetic torques is zero. When the particle angular velocity is different from the fluid rotation rate, the torque exerted by the particles on the fluid results in an antisymmetric particle stress. The stress is of the form 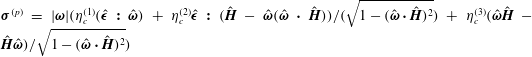 $\unicode[STIX]{x1D748}^{(p)}=|\unicode[STIX]{x1D74E}|(\unicode[STIX]{x1D702}_{c}^{(1)}(\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }\hat{\unicode[STIX]{x1D74E}})+\unicode[STIX]{x1D702}_{c}^{(2)}\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }(\hat{\boldsymbol{H}}-\hat{\unicode[STIX]{x1D74E}}(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}))/(\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})+\unicode[STIX]{x1D702}_{c}^{(3)}(\hat{\unicode[STIX]{x1D74E}}\hat{\boldsymbol{H}}-\hat{\boldsymbol{H}}\hat{\unicode[STIX]{x1D74E}})/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$, where
$\unicode[STIX]{x1D748}^{(p)}=|\unicode[STIX]{x1D74E}|(\unicode[STIX]{x1D702}_{c}^{(1)}(\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }\hat{\unicode[STIX]{x1D74E}})+\unicode[STIX]{x1D702}_{c}^{(2)}\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }(\hat{\boldsymbol{H}}-\hat{\unicode[STIX]{x1D74E}}(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}))/(\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})+\unicode[STIX]{x1D702}_{c}^{(3)}(\hat{\unicode[STIX]{x1D74E}}\hat{\boldsymbol{H}}-\hat{\boldsymbol{H}}\hat{\unicode[STIX]{x1D74E}})/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$, where 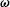 $\unicode[STIX]{x1D74E}$ is the fluid vorticity at the centre of the particle,
$\unicode[STIX]{x1D74E}$ is the fluid vorticity at the centre of the particle, 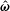 $\hat{\unicode[STIX]{x1D74E}}$ and
$\hat{\unicode[STIX]{x1D74E}}$ and 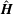 $\hat{\boldsymbol{H}}$ are the unit vectors in the direction of the fluid vorticity and the magnetic field,
$\hat{\boldsymbol{H}}$ are the unit vectors in the direction of the fluid vorticity and the magnetic field, 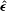 $\hat{\unicode[STIX]{x1D750}}$ is the third order Levi-Civita antisymmetric tensor and
$\hat{\unicode[STIX]{x1D750}}$ is the third order Levi-Civita antisymmetric tensor and 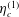 $\unicode[STIX]{x1D702}_{c}^{(1)}$,
$\unicode[STIX]{x1D702}_{c}^{(1)}$, 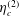 $\unicode[STIX]{x1D702}_{c}^{(2)}$ and
$\unicode[STIX]{x1D702}_{c}^{(2)}$ and  $\unicode[STIX]{x1D702}_{c}^{(3)}$ are called the first, second and third couple stress coefficients. The stress proportional to
$\unicode[STIX]{x1D702}_{c}^{(3)}$ are called the first, second and third couple stress coefficients. The stress proportional to 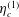 $\unicode[STIX]{x1D702}_{c}^{(1)}$ is in the plane perpendicular to
$\unicode[STIX]{x1D702}_{c}^{(1)}$ is in the plane perpendicular to 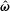 $\hat{\unicode[STIX]{x1D74E}}$, that proportional to
$\hat{\unicode[STIX]{x1D74E}}$, that proportional to 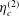 $\unicode[STIX]{x1D702}_{c}^{(2)}$ is in the plane perpendicular to the unit normal to
$\unicode[STIX]{x1D702}_{c}^{(2)}$ is in the plane perpendicular to the unit normal to 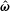 $\hat{\unicode[STIX]{x1D74E}}$ in the
$\hat{\unicode[STIX]{x1D74E}}$ in the 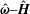 $\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane, and that proportional to
$\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane, and that proportional to 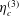 $\unicode[STIX]{x1D702}_{c}^{(3)}$ is in the
$\unicode[STIX]{x1D702}_{c}^{(3)}$ is in the 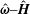 $\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane. A relation
$\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane. A relation 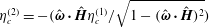 $\unicode[STIX]{x1D702}_{c}^{(2)}=-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\unicode[STIX]{x1D702}_{c}^{(1)}/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$ results from the condition that the component of the eddy current torque along the magnetic field is zero. The couple stress coefficients are obtained for two geometries, a uniform spherical particle of radius
$\unicode[STIX]{x1D702}_{c}^{(2)}=-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\unicode[STIX]{x1D702}_{c}^{(1)}/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$ results from the condition that the component of the eddy current torque along the magnetic field is zero. The couple stress coefficients are obtained for two geometries, a uniform spherical particle of radius 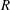 $R$ and a thin spherical shell of radius
$R$ and a thin spherical shell of radius 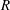 $R$ and thickness
$R$ and thickness 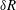 $\unicode[STIX]{x1D6FF}R$ with
$\unicode[STIX]{x1D6FF}R$ with 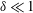 $\unicode[STIX]{x1D6FF}\ll 1$, in the dilute (non-interacting) limit in the absence of fluid inertia. These couple stress coefficients are functions of two dimensionless parameters,
$\unicode[STIX]{x1D6FF}\ll 1$, in the dilute (non-interacting) limit in the absence of fluid inertia. These couple stress coefficients are functions of two dimensionless parameters, 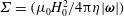 $\unicode[STIX]{x1D6F4}=(\unicode[STIX]{x1D707}_{0}H_{0}^{2}/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}|\unicode[STIX]{x1D74E}|)$, the ratio of the characteristic magnetic and hydrodynamic torques, and
$\unicode[STIX]{x1D6F4}=(\unicode[STIX]{x1D707}_{0}H_{0}^{2}/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}|\unicode[STIX]{x1D74E}|)$, the ratio of the characteristic magnetic and hydrodynamic torques, and 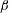 $\unicode[STIX]{x1D6FD}$, the product of the vorticity and current relaxation time. Here
$\unicode[STIX]{x1D6FD}$, the product of the vorticity and current relaxation time. Here 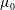 $\unicode[STIX]{x1D707}_{0}$ is the magnetic permeability,
$\unicode[STIX]{x1D707}_{0}$ is the magnetic permeability, 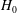 $H_{0}$ is the magnetic field and
$H_{0}$ is the magnetic field and 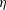 $\unicode[STIX]{x1D702}$ is the fluid viscosity. The parameter
$\unicode[STIX]{x1D702}$ is the fluid viscosity. The parameter 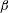 $\unicode[STIX]{x1D6FD}$ has the form
$\unicode[STIX]{x1D6FD}$ has the form 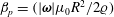 $\unicode[STIX]{x1D6FD}_{p}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}/2\unicode[STIX]{x1D71A})$ for a uniform particle and
$\unicode[STIX]{x1D6FD}_{p}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}/2\unicode[STIX]{x1D71A})$ for a uniform particle and 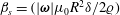 $\unicode[STIX]{x1D6FD}_{s}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}\unicode[STIX]{x1D6FF}/2\unicode[STIX]{x1D71A})$ for a thin shell, where
$\unicode[STIX]{x1D6FD}_{s}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}\unicode[STIX]{x1D6FF}/2\unicode[STIX]{x1D71A})$ for a thin shell, where 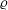 $\unicode[STIX]{x1D71A}$ is the electrical resistivity. Scaled couple stress coefficients are defined,
$\unicode[STIX]{x1D71A}$ is the electrical resistivity. Scaled couple stress coefficients are defined,  $\unicode[STIX]{x1D702}_{1}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(1)}/((3\unicode[STIX]{x1D702}\unicode[STIX]{x1D719}/2)(1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2})))$ and
$\unicode[STIX]{x1D702}_{1}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(1)}/((3\unicode[STIX]{x1D702}\unicode[STIX]{x1D719}/2)(1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2})))$ and 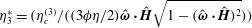 $\unicode[STIX]{x1D702}_{3}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(3)}/((3\unicode[STIX]{x1D719}\unicode[STIX]{x1D702}/2)\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}}))$, which are independent of the fluid viscosity and the particle volume fraction, and which do not depend on
$\unicode[STIX]{x1D702}_{3}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(3)}/((3\unicode[STIX]{x1D719}\unicode[STIX]{x1D702}/2)\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}}))$, which are independent of the fluid viscosity and the particle volume fraction, and which do not depend on 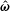 $\hat{\unicode[STIX]{x1D74E}}$ and
$\hat{\unicode[STIX]{x1D74E}}$ and 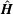 $\hat{\boldsymbol{H}}$ in the limits
$\hat{\boldsymbol{H}}$ in the limits 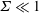 $\unicode[STIX]{x1D6F4}\ll 1$ and
$\unicode[STIX]{x1D6F4}\ll 1$ and 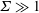 $\unicode[STIX]{x1D6F4}\gg 1$. Here,
$\unicode[STIX]{x1D6F4}\gg 1$. Here, 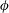 $\unicode[STIX]{x1D719}$ is the volume fraction of the particles. Asymptotic analysis is used to determine the couple stress coefficients in the limits
$\unicode[STIX]{x1D719}$ is the volume fraction of the particles. Asymptotic analysis is used to determine the couple stress coefficients in the limits 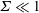 $\unicode[STIX]{x1D6F4}\ll 1$ and
$\unicode[STIX]{x1D6F4}\ll 1$ and 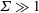 $\unicode[STIX]{x1D6F4}\gg 1$, and a numerical solution procedure is formulated for
$\unicode[STIX]{x1D6F4}\gg 1$, and a numerical solution procedure is formulated for  $\unicode[STIX]{x1D6F4}\sim 1$. For
$\unicode[STIX]{x1D6F4}\sim 1$. For 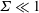 $\unicode[STIX]{x1D6F4}\ll 1$, the particle angular velocity is aligned close to the fluid vorticity, and the scaled couple stress coefficients are
$\unicode[STIX]{x1D6F4}\ll 1$, the particle angular velocity is aligned close to the fluid vorticity, and the scaled couple stress coefficients are 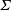 $\unicode[STIX]{x1D6F4}$ times a function of
$\unicode[STIX]{x1D6F4}$ times a function of 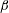 $\unicode[STIX]{x1D6FD}$. For
$\unicode[STIX]{x1D6FD}$. For 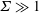 $\unicode[STIX]{x1D6F4}\gg 1$, the particle angular velocity is aligned close to the magnetic field,
$\unicode[STIX]{x1D6F4}\gg 1$, the particle angular velocity is aligned close to the magnetic field, 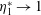 $\unicode[STIX]{x1D702}_{1}^{\ast }\rightarrow 1$ and
$\unicode[STIX]{x1D702}_{1}^{\ast }\rightarrow 1$ and 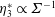 $\unicode[STIX]{x1D702}_{3}^{\ast }\propto \unicode[STIX]{x1D6F4}^{-1}$. When the magnetic field is perpendicular to the fluid vorticity,
$\unicode[STIX]{x1D702}_{3}^{\ast }\propto \unicode[STIX]{x1D6F4}^{-1}$. When the magnetic field is perpendicular to the fluid vorticity, 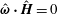 $\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}=0$, the particle angular velocity is aligned along the vorticity, and only the first couple stress coefficient is non-zero. For high
$\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}=0$, the particle angular velocity is aligned along the vorticity, and only the first couple stress coefficient is non-zero. For high 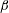 $\unicode[STIX]{x1D6FD}$, there are multiple solutions for the couple stress coefficient. Multiple steady states are also observed for a near perpendicular magnetic field,
$\unicode[STIX]{x1D6FD}$, there are multiple solutions for the couple stress coefficient. Multiple steady states are also observed for a near perpendicular magnetic field, 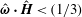 $\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}<(1/3)$, for a reason different from that for a perpendicular magnetic field. Asymptotic analysis is used to explain the existence of multiple steady states in both cases.
$\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}<(1/3)$, for a reason different from that for a perpendicular magnetic field. Asymptotic analysis is used to explain the existence of multiple steady states in both cases.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 10
- Cited by

