Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2014.
Transition of natural convection boundary layers—a revisit by Bicoherence analysis.
International Communications in Heat and Mass Transfer,
Vol. 58,
Issue. ,
p.
147.
Liu, Yang
Lei, Chengwang
and
Patterson, John C.
2014.
Natural convection in a differentially heated cavity with two horizontal adiabatic fins on the sidewalls.
International Journal of Heat and Mass Transfer,
Vol. 72,
Issue. ,
p.
23.
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2015.
A PIV measurement of the natural transition of a natural convection boundary layer.
Experiments in Fluids,
Vol. 56,
Issue. 1,
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2016.
Natural transition in natural convection boundary layers.
International Communications in Heat and Mass Transfer,
Vol. 76,
Issue. ,
p.
366.
Salari, Mahmoud
Rashidi, Mohammad Mehdi
Hasani Malekshah, Emad
and
Hasani Malekshah, Masoud
2017.
Numerical analysis of turbulent/transitional natural convection in trapezoidal enclosures.
International Journal of Numerical Methods for Heat & Fluid Flow,
Vol. 27,
Issue. 12,
p.
2902.
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2017.
The K-type and H-type transitions of natural convection boundary layers.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
352.
Kouroudis, Ioannis
Saliakellis, Panagiotis
and
Yiantsios, Stergios G.
2017.
Direct numerical simulation of natural convection in a square cavity with uniform heat fluxes at the vertical sides: Flow structure and transition.
International Journal of Heat and Mass Transfer,
Vol. 115,
Issue. ,
p.
428.
Chorin, Paul
Moreau, Florian
and
Saury, Didier
2018.
Heat transfer modification induced by a localized thermal disturbance in a differentially-heated cavity.
International Journal of Thermal Sciences,
Vol. 125,
Issue. ,
p.
101.
Schaub, Michael
Kriegel, Martin
and
Brandt, Stefan
2019.
Analytical prediction of heat transfer by unsteady natural convection at vertical flat plates in air.
International Journal of Heat and Mass Transfer,
Vol. 144,
Issue. ,
p.
118665.
Schaub, Michael
Kriegel, Martin
and
Brandt, Stefan
2019.
Experimental investigation of heat transfer by unsteady natural convection at a vertical flat plate.
International Journal of Heat and Mass Transfer,
Vol. 136,
Issue. ,
p.
1186.
Zhao, Yongling
Zhao, Pengpeng
Liu, Yang
Xu, Yin
and
Torres, Juan F.
2019.
On the selection of perturbations for thermal boundary layer control.
Physics of Fluids,
Vol. 31,
Issue. 10,
Liu, Yang
Bian, Yongning
Zhao, Yongling
Zhang, Shuaikun
and
Suo, Qinghui
2019.
Scaling laws for the transient convective flow in a differentially and linearly heated rectangular cavity at Pr > 1.
Physics of Fluids,
Vol. 31,
Issue. 4,
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2019.
PIV measurements of the K-type transition in natural convection boundary layers.
Experimental Thermal and Fluid Science,
Vol. 101,
Issue. ,
p.
62.
Liu, Yang
2019.
Scaling of convective boundary layer flow induced by linear thermal forcing at
Pr<1
and
Pr>1.
Physical Review E,
Vol. 100,
Issue. 4,
Villa Ortiz, Agustín
and
Koloszar, Lilla
2020.
Application of numerical transition control method to enhance turbulence in a natural convection boundary layer over a vertical heated plate.
Computers & Fluids,
Vol. 199,
Issue. ,
p.
104417.
Wan, Zhenping
He, Zicong
Wang, Xiaowu
chen, Boqian
Ong, Robert H.
and
Zhao, Yongling
2020.
Heat transfer in a liquid under focused ultrasonic field.
Experimental Thermal and Fluid Science,
Vol. 119,
Issue. ,
p.
110179.
Ke, Junhao
Williamson, N.
Armfield, S. W.
Norris, S. E.
and
Komiya, A.
2020.
Law of the wall for a temporally evolving vertical natural convection boundary layer.
Journal of Fluid Mechanics,
Vol. 902,
Issue. ,
Zhang, Zhihao
Wang, Xuehui
and
Yan, Yuying
2021.
A review of the state-of-the-art in electronic cooling.
e-Prime - Advances in Electrical Engineering, Electronics and Energy,
Vol. 1,
Issue. ,
p.
100009.
Ogasawara, Naoto
Torres, Juan F.
Kanda, Yuki
Kogawa, Takuma
and
Komiya, Atsuki
2021.
Resonance-driven heat transfer enhancement in a natural convection boundary layer perturbed by a moderate impinging jet.
Physical Review Fluids,
Vol. 6,
Issue. 6,
Fan, Yifan
Zhao, Yongling
Torres, Juan F.
Xu, Feng
Lei, Chengwang
Li, Yuguo
and
Carmeliet, Jan
2021.
Natural convection over vertical and horizontal heated flat surfaces: A review of recent progress focusing on underpinnings and implications for heat transfer and environmental applications.
Physics of Fluids,
Vol. 33,
Issue. 10,
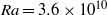 $\mathit{Ra}= 3. 6\times 1{0}^{10} $ and
$\mathit{Ra}= 3. 6\times 1{0}^{10} $ and 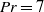 $\mathit{Pr}= 7$ , a net heat transfer enhancement of up to 44 % is achieved by triggering resonance of the boundary layer. This significant enhancement of heat transfer is due to the resonance-induced advancement of the laminar–turbulent transition, which is found to be dependent on the perturbation frequency and amplitude. Evidence from different perspectives revealing the same position of the transition are provided and discussed. The outcomes of this investigation demonstrate the prospect of a resonance-based approach for enhancing heat transfer.
$\mathit{Pr}= 7$ , a net heat transfer enhancement of up to 44 % is achieved by triggering resonance of the boundary layer. This significant enhancement of heat transfer is due to the resonance-induced advancement of the laminar–turbulent transition, which is found to be dependent on the perturbation frequency and amplitude. Evidence from different perspectives revealing the same position of the transition are provided and discussed. The outcomes of this investigation demonstrate the prospect of a resonance-based approach for enhancing heat transfer.
