Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mommert, Michael
Schiepel, Daniel
Schmeling, Daniel
and
Wagner, Claus
2020.
Reversals of coherent structures in turbulent mixed convection.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Kar, Prabir Kumar
Kumar, Yada Nandu
Das, P. K.
and
Lakkaraju, Rajaram
2020.
Thermal convection in octagonal-shaped enclosures.
Physical Review Fluids,
Vol. 5,
Issue. 10,
Liu, Shuang
and
Huisman, Sander G.
2020.
Heat transfer enhancement in Rayleigh-Bénard convection using a single passive barrier.
Physical Review Fluids,
Vol. 5,
Issue. 12,
Zhu, Xu
and
Zhou, Quan
2021.
Flow structures of turbulent Rayleigh–Bénard convection in annular cells with aspect ratio one and larger.
Acta Mechanica Sinica,
Vol. 37,
Issue. 8,
p.
1291.
Xu, Ao
Chen, Xin
and
Xi, Heng-Dong
2021.
Tristable flow states and reversal of the large-scale circulation in two-dimensional circular convection cells.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Cheng, Jie-Jie
Wu, Jian-Zhao
Liu, Yu-Lu
and
Lu, Zhi-Ming
2021.
Sidewall controlling large-scale flow structure and reversal in turbulent Rayleigh-Bénard convection.
Journal of Turbulence,
Vol. 22,
Issue. 6,
p.
380.
Zhang, Shengqi
Chen, Xin
Xia, Zhenhua
Xi, Heng-Dong
Zhou, Quan
and
Chen, Shiyi
2021.
Stabilizing/destabilizing the large-scale circulation in turbulent Rayleigh–Bénard convection with sidewall temperature control.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Zhao, Chao-Ben
Wang, Bo-Fu
Wu, Jian-Zhao
Chong, Kai Leong
and
Zhou, Quan
2022.
Suppression of flow reversals via manipulating corner rolls in plane Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Li, Yi-Zhen
Chen, Xin
Xu, Ao
and
Xi, Heng-Dong
2022.
Counter-flow orbiting of the vortex centre in turbulent thermal convection.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Wang, Dongpu
Liu, Shuang
Zhou, Quan
and
Sun, Chao
2022.
Spectra and structure functions of the temperature and velocity fields in supergravitational thermal turbulence.
Physics of Fluids,
Vol. 34,
Issue. 5,
Wang, Dongpu
Jiang, Hechuan
Liu, Shuang
Zhu, Xiaojue
and
Sun, Chao
2022.
Effects of radius ratio on annular centrifugal Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Sun, Yu
Xie, Yi-Chao
Xie, Jin-Xiao
Zhong, Jin-Qiang
Zhang, Jianwei
and
Xia, Ke-Qing
2024.
Model for the dynamics of the large-scale circulations in two-layer turbulent convection.
Physical Review Fluids,
Vol. 9,
Issue. 3,
Hu, Jin
Zhang, Shengqi
and
Xia, Zhenhua
2024.
Flow reversal and multiple states in turbulent Rayleigh–Bénard convection with partially isothermal plates.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Chen, Xin-Yuan
Yang, Juan-Cheng
and
Ni, Ming-Jiu
2024.
Effects of horizontal magnetic fields on flow morphologies and global transports in liquid metal thermal convection.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Wang, Dongpu
Liu, Jing
Lai, Rushi
and
Sun, Chao
2024.
Temperature fluctuations and heat transport in partitioned supergravitational thermal turbulence.
Acta Mechanica Sinica,
Vol. 40,
Issue. 6,
Wang, Ze-Hao
Chen, Xin
Xu, Ao
and
Xi, Heng-Dong
2024.
Prandtl number dependence of flow topology in quasi-two-dimensional turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 991,
Issue. ,
Kashanj, Sina
and
Nobes, David S.
2024.
Temperature field of non-Oberbeck–Boussinesq Rayleigh–Bénard convection in a low aspect ratio cell.
Physics of Fluids,
Vol. 36,
Issue. 4,
Zhao, Hao-Bo
Zhao, Chao-Ben
Zhou, Quan
and
Chong, Kai Leong
2024.
Thermal convection modulated by actively oscillating filament: The effect of filament rigidity.
International Journal of Heat and Mass Transfer,
Vol. 228,
Issue. ,
p.
125649.
Huang, Ze-Lin
Wu, Jian-Zhao
Guo, Xi-Li
Zhao, Chao-Ben
Wang, Bo-Fu
Chong, Kai Leong
and
Zhou, Quan
2024.
Unifying constitutive law of vibroconvective turbulence in microgravity.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Li, Yi-Zhen
Chen, Xin
and
Xi, Heng-Dong
2024.
Enhanced heat transfer and reduced flow reversals in turbulent thermal convection with an obstructed centre.
Journal of Fluid Mechanics,
Vol. 981,
Issue. ,
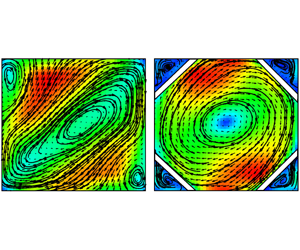
 $Ra$, separated by a transitional
$Ra$, separated by a transitional  $Ra$ (
$Ra$ ( $Ra_{t,r}$). The transition is similar to that in the normal cell, and
$Ra_{t,r}$). The transition is similar to that in the normal cell, and  $Ra_{t,r}$ is almost the same for both cells. Despite the similarities, the reversal frequency is greatly reduced in the corner-less cell. The reduction of the reversal frequency is more significant, in terms of both the amplitude and the scaling exponent, in the high-
$Ra_{t,r}$ is almost the same for both cells. Despite the similarities, the reversal frequency is greatly reduced in the corner-less cell. The reduction of the reversal frequency is more significant, in terms of both the amplitude and the scaling exponent, in the high- $Ra$ regime. In addition, we classified the reversals into main-vortex-led and corner-vortex-led, and found that both types exist in the normal cell while only the former exists in the corner-less cell. The frequency of main-vortex-led reversal in the normal cell is found to be in excellent agreement with the frequency of reversals in the corner-less cell. Our results reveal for the first time the quantitative role of the corner vortices in the occurrence of the reversals of the large-scale circulation.
$Ra$ regime. In addition, we classified the reversals into main-vortex-led and corner-vortex-led, and found that both types exist in the normal cell while only the former exists in the corner-less cell. The frequency of main-vortex-led reversal in the normal cell is found to be in excellent agreement with the frequency of reversals in the corner-less cell. Our results reveal for the first time the quantitative role of the corner vortices in the occurrence of the reversals of the large-scale circulation.
