Article contents
Rapid distortion theory analysis on the interaction between homogeneous turbulence and a planar shock wave
Published online by Cambridge University Press: 01 August 2016
Abstract
The interactions between homogeneous turbulence and a planar shock wave are analytically investigated using rapid distortion theory (RDT). Analytical solutions in the solenoidal modes are obtained. Qualitative answers to unsolved questions in a report by Andreopoulos et al. (Annu. Rev. Fluid Mech., vol. 524, 2000, pp. 309–345) are provided within the linear theoretical framework. The results show that the turbulence kinetic energy (TKE) is increased after interaction with a shock wave and that the contributions to the amplification can be interpreted primarily as the combined effect of shock-induced compression, which is a direct consequence of the Rankine–Hugoniot relation, and the nonlinear effect, which is an indirect consequence of the Rankine–Hugoniot relation via the perturbation manner. For initial homogeneous axisymmetric turbulence, the amplification of the TKE depends on the initial degree of anisotropy. Furthermore, the increase in energy at high wavenumbers is confirmed by the one-dimensional spectra. The enstrophy is also increased; its increase is more significant than that of the TKE because of the significant increase in enstrophy at high wavenumbers. The vorticity components perpendicular to the shock-induced compressed direction are amplified more than the parallel vorticity component. These results strongly suggest that a high resolution is needed to obtain accurate results for the turbulence–shock-wave interaction. The integral length scales ( 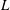 $L$ ) and the Taylor microscales (
$L$ ) and the Taylor microscales ( 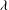 $\unicode[STIX]{x1D706}$ ) are decreased for most cases after the interaction. However,
$\unicode[STIX]{x1D706}$ ) are decreased for most cases after the interaction. However, 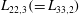 $L_{22,3}(=\,L_{33,2})$ and
$L_{22,3}(=\,L_{33,2})$ and 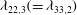 $\unicode[STIX]{x1D706}_{22,3}(=\,\unicode[STIX]{x1D706}_{33,2})$ are amplified. Here, the subscripts 2 and 3 indicate the perpendicular components relative to the shock-induced compressed direction. The dissipation length and TKE dissipation rate are amplified.
$\unicode[STIX]{x1D706}_{22,3}(=\,\unicode[STIX]{x1D706}_{33,2})$ are amplified. Here, the subscripts 2 and 3 indicate the perpendicular components relative to the shock-induced compressed direction. The dissipation length and TKE dissipation rate are amplified.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 12
- Cited by


