Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dogan, Mine
Moysey, Stephen M. J.
Ramakers, Ruud M.
DeVol, Timothy A.
Beekman, Frederik J.
Groen, Harald C.
and
Powell, Brian A.
2017.
High-Resolution 4D Preclinical Single-Photon Emission Computed Tomography/X-ray Computed Tomography Imaging of Technetium Transport within a Heterogeneous Porous Media.
Environmental Science & Technology,
Vol. 51,
Issue. 5,
p.
2864.
Zahasky, Christopher
and
Benson, Sally M.
2017.
Using Micro-positron Emission Tomography to Quantify Single and Multiphase Flow in Heterogeneous Reservoirs.
Energy Procedia,
Vol. 114,
Issue. ,
p.
5070.
Pini, Ronny
and
Benson, Sally M
2017.
Capillary pressure heterogeneity and hysteresis for the supercritical CO2/water system in a sandstone.
Advances in Water Resources,
Vol. 108,
Issue. ,
p.
277.
Boon, Maartje
Bijeljic, Branko
and
Krevor, Samuel
2017.
Observations of the impact of rock heterogeneity on solute spreading and mixing.
Water Resources Research,
Vol. 53,
Issue. 6,
p.
4624.
Kulenkampff, Johannes
Stoll, Madeleine
Gründig, Marion
Mansel, Alexander
Lippmann-Pipke, Johanna
and
Kersten, Michael
2018.
Time-lapse 3D imaging by positron emission tomography of Cu mobilized in a soil column by the herbicide MCPA.
Scientific Reports,
Vol. 8,
Issue. 1,
Zahasky, Christopher
and
Benson, Sally M.
2018.
Micro-positron emission tomography for measuring sub-core scale single and multiphase transport parameters in porous media.
Advances in Water Resources,
Vol. 115,
Issue. ,
p.
1.
Zahasky, Christopher
Thomas, Dana
Matter, Juerg
Maher, Kate
and
Benson, Sally M.
2018.
Multimodal imaging and stochastic percolation simulation for improved quantification of effective porosity and surface area in vesicular basalt.
Advances in Water Resources,
Vol. 121,
Issue. ,
p.
235.
Kurotori, Takeshi
Zahasky, Christopher
Hosseinzadeh Hejazi, Sayed Alireza
Shah, Saurabh M.
Benson, Sally M.
and
Pini, Ronny
2019.
Measuring, imaging and modelling solute transport in a microporous limestone.
Chemical Engineering Science,
Vol. 196,
Issue. ,
p.
366.
Pini, Ronny
and
Krevor, Samuel
2019.
Science of Carbon Storage in Deep Saline Formations.
p.
145.
Dou, Zhi
Zhang, Xueyi
Chen, Zhou
Yang, Yun
Zhuang, Chao
and
Wang, Chenxi
2019.
Effects of Cemented Porous Media on Temporal Mixing Behavior of Conservative Solute Transport.
Water,
Vol. 11,
Issue. 6,
p.
1204.
Zahasky, Christopher
Kurotori, Takeshi
Pini, Ronny
and
Benson, Sally M.
2019.
Positron emission tomography in water resources and subsurface energy resources engineering research.
Advances in Water Resources,
Vol. 127,
Issue. ,
p.
39.
Luttge, Andreas
Arvidson, Rolf S.
Fischer, Cornelius
and
Kurganskaya, Inna
2019.
Kinetic concepts for quantitative prediction of fluid-solid interactions.
Chemical Geology,
Vol. 504,
Issue. ,
p.
216.
Akono, Ange‐Therese
Druhan, Jennifer L.
Dávila, Gabriela
Tsotsis, Theodore
Jessen, Kristian
Fuchs, Samantha
Crandall, Dustin
Shi, Zhuofan
Dalton, Laura
Tkach, Mary K.
Goodman, Angela L.
Frailey, Scott
and
Werth, Charles J.
2019.
A review of geochemical–mechanical impacts in geological carbon storage reservoirs.
Greenhouse Gases: Science and Technology,
Vol. 9,
Issue. 3,
p.
474.
Brattekås, B.
Gauteplass, J.
Brekke, N.
Fernø, M.A.
and
Ersland, G.
2020.
Unlocking multimodal PET-MR synergies for geoscience.
Advances in Water Resources,
Vol. 142,
Issue. ,
p.
103641.
Brattekås, Bergit
and
Haugen, Malin
2020.
Explicit tracking of CO2-flow at the core scale using micro-Positron Emission Tomography (μPET).
Journal of Natural Gas Science and Engineering,
Vol. 77,
Issue. ,
p.
103268.
Hu, Yibing
Armstrong, Ryan T.
Shikhov, Igor
Hung, Tzong T.
Lee, Brendan
and
Mostaghimi, Peyman
2020.
Unsteady-State Coreflooding Monitored by Positron Emission Tomography and X-ray Computed Tomography.
SPE Journal,
Vol. 25,
Issue. 01,
p.
242.
Brattekås, Bergit
and
Seright, Randy
2020.
The Mechanism for Improved Polymer Gel Blocking During Low-Salinity Waterfloods, Investigated Using Positron Emission Tomography Imaging.
Transport in Porous Media,
Vol. 133,
Issue. 1,
p.
119.
Jahanbakhsh, Amir
Wlodarczyk, Krystian L.
Hand, Duncan P.
Maier, Robert R. J.
and
Maroto-Valer, M. Mercedes
2020.
Review of Microfluidic Devices and Imaging Techniques for Fluid Flow Study in Porous Geomaterials.
Sensors,
Vol. 20,
Issue. 14,
p.
4030.
Dara, Mojtaba
Kazemi, Zahra
and
Samadfam, Mohammad
2020.
A new method for determination of concentration profile in a transport column by gamma spectroscopy combined with genetic algorithm.
Progress in Nuclear Energy,
Vol. 124,
Issue. ,
p.
103346.
Kurotori, Takeshi
Zahasky, Christopher
Benson, Sally M.
and
Pini, Ronny
2020.
Description of Chemical Transport in Laboratory Rock Cores Using the Continuous Random Walk Formalism.
Water Resources Research,
Vol. 56,
Issue. 9,
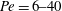 $Pe=6{-}40$ and are supplemented by a unique combination of two imaging techniques. X-ray computed tomography (CT) is used to quantify subcore-scale heterogeneities in terms of permeability contrasts at a spatial resolution of approximately
$Pe=6{-}40$ and are supplemented by a unique combination of two imaging techniques. X-ray computed tomography (CT) is used to quantify subcore-scale heterogeneities in terms of permeability contrasts at a spatial resolution of approximately 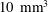 $10~\text{mm}^{3}$ , while [11C] positron emission tomography (PET) is applied to image the spatial and temporal evolution of the full tracer plume non-invasively. To account for both advective spreading and local (Fickian) mixing as driving mechanisms for solute transport, a streamtube model is applied that is based on the one-dimensional advection–dispersion equation. We refer to our modelling approach as semideterministic, because the spatial arrangement of the streamtubes and the corresponding solute travel times are known from the measured rock’s permeability map, which required only small adjustments to match the measured tracer breakthrough curve. The model reproduces the three-dimensional PET measurements accurately by capturing the larger-scale tracer plume deformation as well as subcore-scale mixing, while confirming negligible transverse dispersion over the scale of the experiment. We suggest that the obtained longitudinal dispersivity (
$10~\text{mm}^{3}$ , while [11C] positron emission tomography (PET) is applied to image the spatial and temporal evolution of the full tracer plume non-invasively. To account for both advective spreading and local (Fickian) mixing as driving mechanisms for solute transport, a streamtube model is applied that is based on the one-dimensional advection–dispersion equation. We refer to our modelling approach as semideterministic, because the spatial arrangement of the streamtubes and the corresponding solute travel times are known from the measured rock’s permeability map, which required only small adjustments to match the measured tracer breakthrough curve. The model reproduces the three-dimensional PET measurements accurately by capturing the larger-scale tracer plume deformation as well as subcore-scale mixing, while confirming negligible transverse dispersion over the scale of the experiment. We suggest that the obtained longitudinal dispersivity ( 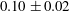 $0.10\pm 0.02$ cm) is rock rather than sample specific, because of the ability of the model to decouple subcore-scale permeability heterogeneity effects from those of local dispersion. As such, the approach presented here proves to be very valuable, if not necessary, in the context of reservoir core analyses, because rock samples can rarely be regarded as ‘uniformly heterogeneous’.
$0.10\pm 0.02$ cm) is rock rather than sample specific, because of the ability of the model to decouple subcore-scale permeability heterogeneity effects from those of local dispersion. As such, the approach presented here proves to be very valuable, if not necessary, in the context of reservoir core analyses, because rock samples can rarely be regarded as ‘uniformly heterogeneous’.

