Article contents
Quantifying eddy structures and very-large-scale motions in turbulent round jets
Published online by Cambridge University Press: 06 April 2021
Abstract
Coherent structures in turbulent round jets are evaluated for a jet Reynolds number up to  $Re_d=50\,000$ with the aid of two-point measurements and an existing direct numerical simulation (DNS) dataset at
$Re_d=50\,000$ with the aid of two-point measurements and an existing direct numerical simulation (DNS) dataset at  $Re_d=7290$. The experimental data comprise simultaneous velocity time series acquired with both radial and azimuthal separations between the sensors. A spectral correlation analysis is applied to these data that reveals that the coherent structures in the jet flow consist of two principal configurations, which correspond to two main spectral domains. One spectral domain, which is signified by small to medium wavelengths, is associated with hierarchical eddy structures (ESs) for which a physical aspect ratio of
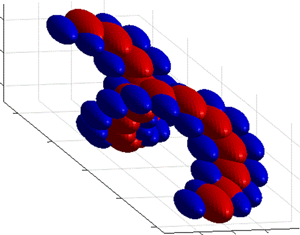
$Re_d=7290$. The experimental data comprise simultaneous velocity time series acquired with both radial and azimuthal separations between the sensors. A spectral correlation analysis is applied to these data that reveals that the coherent structures in the jet flow consist of two principal configurations, which correspond to two main spectral domains. One spectral domain, which is signified by small to medium wavelengths, is associated with hierarchical eddy structures (ESs) for which a physical aspect ratio of  $1.2:1:1$ in the axial, radial and azimuthal directions is observed. The other spectral domain, indicated by large wavelengths, is associated with very-large-scale motions (VLSMs). The wavelength marking the boundary between these spectral domains is used to decompose the velocity fluctuations into ES and VLSM components, and the corresponding ES and VLSM components of two-point correlations are obtained from the experimental data. The VLSM component of two-point correlations denotes helical structures as the dominant VLSMs in the jet turbulent region. Instantaneous axial velocity fluctuation fields from DNS support the prevalence of helical VLSMs in the jet. Moreover, the ES signatures are evident in the unwrapped axial–azimuthal planes of the DNS, indicating that the VLSMs are formed by the concatenation of ESs. Consistent with the experimental two-point correlations and DNS flow fields, a conceptual model is proposed for the ESs and VLSMs, which illustrates their arrangements.
$1.2:1:1$ in the axial, radial and azimuthal directions is observed. The other spectral domain, indicated by large wavelengths, is associated with very-large-scale motions (VLSMs). The wavelength marking the boundary between these spectral domains is used to decompose the velocity fluctuations into ES and VLSM components, and the corresponding ES and VLSM components of two-point correlations are obtained from the experimental data. The VLSM component of two-point correlations denotes helical structures as the dominant VLSMs in the jet turbulent region. Instantaneous axial velocity fluctuation fields from DNS support the prevalence of helical VLSMs in the jet. Moreover, the ES signatures are evident in the unwrapped axial–azimuthal planes of the DNS, indicating that the VLSMs are formed by the concatenation of ESs. Consistent with the experimental two-point correlations and DNS flow fields, a conceptual model is proposed for the ESs and VLSMs, which illustrates their arrangements.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 9
- Cited by


