Published online by Cambridge University Press: 04 December 2024
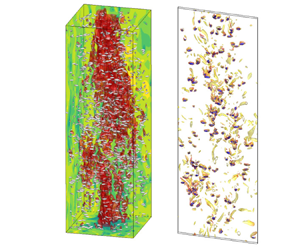
In this study we investigate the sedimentation of prolate spheroids in a quiescent fluid by means of the particle-resolved direct numerical simulation. With the increase of the particle volume fraction  $\phi$ from
$\phi$ from  $0.1\,\%$ to
$0.1\,\%$ to  $10\,\%$, we observe a non-monotonic variation of the mean settling velocity of particles,
$10\,\%$, we observe a non-monotonic variation of the mean settling velocity of particles,  $\langle V_s \rangle$. By virtue of the Voronoi analysis, we find that the degree of particle clustering is highest when
$\langle V_s \rangle$. By virtue of the Voronoi analysis, we find that the degree of particle clustering is highest when  $\langle V_s \rangle$ reaches the local maximum at
$\langle V_s \rangle$ reaches the local maximum at  $\phi =1\,\%$. Under the swarm effect, clustered particles are found to preferentially sample downward fluid flows in the wake regions, leading to the enhancement of the settling speed. As for lower or higher volume fractions, the tendency of particle clustering and the preferential sampling of downward flows are attenuated. The hindrance effect becomes predominant when the volume fraction exceeds 5 % and reduces
$\phi =1\,\%$. Under the swarm effect, clustered particles are found to preferentially sample downward fluid flows in the wake regions, leading to the enhancement of the settling speed. As for lower or higher volume fractions, the tendency of particle clustering and the preferential sampling of downward flows are attenuated. The hindrance effect becomes predominant when the volume fraction exceeds 5 % and reduces  $\langle V_s \rangle$ to less than the isolated settling velocity. Particle orientation plays a minor role in the mean settling velocity, although individual prolate particles still tend to settle faster in suspensions when they deviate more from the broad-side-on alignment. Moreover, we also demonstrate that particles are prone to form column-like microstructures in dilute suspensions under the effect of wake-induced hydrodynamic attractions. The radial distribution function is higher at a lower volume fraction. As a result, the collision rate scaled by the particle number density decreases with the increasing volume fraction. By contrast, as another contribution to the particle collision rate, the relative radial velocity for nearby particles shows a minor degree of variation due to the lubrication effect.
$\langle V_s \rangle$ to less than the isolated settling velocity. Particle orientation plays a minor role in the mean settling velocity, although individual prolate particles still tend to settle faster in suspensions when they deviate more from the broad-side-on alignment. Moreover, we also demonstrate that particles are prone to form column-like microstructures in dilute suspensions under the effect of wake-induced hydrodynamic attractions. The radial distribution function is higher at a lower volume fraction. As a result, the collision rate scaled by the particle number density decreases with the increasing volume fraction. By contrast, as another contribution to the particle collision rate, the relative radial velocity for nearby particles shows a minor degree of variation due to the lubrication effect.