1. Introduction
Thermoacoustic instabilities are self-sustained oscillations (Balasubramanian & Sujith Reference Balasubramanian and Sujith2008; Liu, Cheng & Du Reference Liu, Cheng and Du2022) where acoustic waves and unsteady heat release compose a positive feedback loop (Bragg Reference Bragg1964; Dowling Reference Dowling1995; Lyu, Fang & Wang Reference Lyu, Fang and Wang2023). These fluctuations can become intense and cause performance degradation, emission deterioration (Zhang et al. Reference Zhang, Tao, Song, Han, Li, Liu and Qi2023), severe noise (Su, Yang & Morgans Reference Su, Yang and Morgans2022), lifespan reduction, structural damage, and even catastrophic machine failure in propulsive systems or power generation units. Thus acquiring control methods to prevent or restrict such undesirable high-amplitude oscillations of the self-excited system is of great significance (Juniper & Sujith Reference Juniper and Sujith2018; Sun et al. Reference Sun, Zhao, Ji, Zhu, Rao and Wang2022).
Many studies (Dowling & Morgans Reference Dowling and Morgans2005; Zhao & Li Reference Zhao and Li2015; Guan et al. Reference Guan, Li, Jegal and Kim2023) have underlined the importance of suppressing pressure oscillations. Passive control methods, such as perforated liners, baffles, and half- and quarter-wave tubes, have been employed to dissipate pressure fluctuations effectively (Zhao & Morgans Reference Zhao and Morgans2009; Zhao Reference Zhao and Zhao2023b). Active control (Zhang et al. Reference Zhang, Li, Cheng and Li2020; Naji et al. Reference Naji, Rahimi, Bazargan and Marengo2023), such as feedback control (Zhao & Reyhanoglu Reference Zhao and Reyhanoglu2014), open (Wu et al. Reference Wu, Xu, Li and Ji2019) or close-loop active control (McManus, Poinsot & Candel Reference McManus, Poinsot and Candel1993; Zhao Reference Zhao and Zhao2023a), and adaptive control (Zhao Reference Zhao and Zhao2023a), can suppress undesired instabilities through activatable devices. Their practical implementation is limited by the installation of feedback devices (Balusamy et al. Reference Balusamy, Li, Han, Juniper and Hochgreb2015; Biwa et al. Reference Biwa, Sawada, Hyodo and Kato2016). Therefore, a recently proposed approach, which controls pressure oscillations in coupled systems, attracted the authors’ attention. Based on the amplitude death (AD) theory, which has been validated against experiments (Zhao et al. Reference Zhao, Ji, Li and Li2015; Sahay et al. Reference Sahay, Roy, Pawar and Sujith2021), coupling two systems using a needle valve and a vinyl tube can entirely suppress the unwanted oscillations (Biwa, Tozuka & Yazaki Reference Biwa, Tozuka and Yazaki2015; Thomas et al. Reference Thomas, Mondal, Pawar and Sujith2018; Srikanth et al. Reference Srikanth, Sahay, Pawar, Manoj and Sujith2022). For the design of coupled systems, the description of the non-normality and nonlinearity characteristics (Yang, Pang & Li Reference Yang, Pang and Li2021; Wu et al. Reference Wu, Nan, Yang and Li2023) by partial differential equations (PDEs) is essential. However, the complexity of engineering systems challenges the derivation of PDEs for such applications.
The van der Pol (VDP) equation is a reliable alternative to formulate deterministic system descriptions, which has been studied extensively (Nbendjo & Yamapi Reference Nbendjo and Yamapi2007; Yamapi, Nana Nbendjo & Kadji Reference Yamapi, Nana Nbendjo and Enjieu Kadji2007; Vinod & Balaram Reference Vinod and Balaram2023) owing to its capacity to mimic the nonlinear thermoacoustic instability behaviour on account of its adherence to the Liénard theorem (Perko Reference Perko2013). According to Guan et al. (Reference Guan, Moon, Kim and Li2021), the low-order oscillator model consisting of two simple VDP oscillators can reproduce many synchronization phenomena, including AD characteristics. Next, once the VDP equation is established, the unknown parameters need to be determined from the available data. The recently developed physics-informed neural networks (PINNs) model solves PDEs via deep learning (Raissi, Perdikaris & Karniadakis Reference Raissi, Perdikaris and Karniadakis2017a,Reference Raissi, Perdikaris and Karniadakisb; Lu et al. Reference Lu, Meng, Mao and Karniadakis2021; Wang et al. Reference Wang, Wen, Hu and Wang2023), and has been applied to fluid mechanics and thermoacoustics problems (Mariappan, Nath & Karniadakis Reference Mariappan, Nath and Karniadakis2023; Ozan & Magri Reference Ozan, Magri and Gibbs2023). Thereby, novel perspectives opened up to determine the unknown parameters of inverse problems. That is, incomplete PDEs can be predicted using relatively few experimental measurements (Aliakbari et al. Reference Aliakbari, Soltany Sadrabadi, Vadasz and Arzani2023; Xu et al. Reference Xu, Yan, Zhang, Sun, Huang, Ju, Guo and Yang2023) to replace prohibitively expensive methods in inverse flow problems (Cai et al. Reference Cai, Mao, Wang, Yin and Karniadakis2021).
The horizontal Rijke tube is a simplistic and thermoacoustic unstable system where PDEs can describe its behaviour. On the contrary, the thermoacoustic behaviour of engineering systems – e.g. thermoacoustic engines (TAEs), afterburners, Ramjet engines, and rocket motors – can be assessed only by experimental measurements. The derivation of specific PDEs for controlling strategy estimation of such complex systems is impossible. Thus we present a methodology based on the PINNs algorithm to determine a system instability behaviour by precise differential equations. The proposed extended VDP (EVDP)-PINNs method is validated against theoretical and simulation data, exhibiting acceptable errors. Additionally, the Hopf bifurcation and AD characteristics of the coupled EVDP systems are computed and compared with the coupled theoretical Rijke tube systems. Thereby, the physical significance of the EVDP system in the field of thermoacoustics is shown. Combining the results of the averaging method and the generalized scaling method with the AD boundary analysis provides each term in the EVDP system with a physical significance.
2. Methods
2.1. The EVDP system
The dimensionless pressure perturbation of a combustion system, as plotted in figure 1(a), exhibits a pronounced non-normal system behaviour, where a high-amplitude limit cycle establishes from an initially small perturbation. To replicate such system characteristics, the VDP equation is selected (Nbendjo & Yamapi Reference Nbendjo and Yamapi2007; Yamapi et al. Reference Yamapi, Nana Nbendjo and Enjieu Kadji2007; Vinod & Balaram Reference Vinod and Balaram2023). The non-conservative oscillator with nonlinear damping can be written in its basic form without source term as
where ![]() $\psi$ is the investigated quantity, the dot over the variable represents the temporal derivative, and
$\psi$ is the investigated quantity, the dot over the variable represents the temporal derivative, and ![]() $\mu$ is a parameter defining the nonlinearity and damping strength. The classical VDP oscillator with
$\mu$ is a parameter defining the nonlinearity and damping strength. The classical VDP oscillator with ![]() $\mu =0.2$ resembles the dimensionless pressure perturbation as shown in figure 1, proving that the classical VDP equation can mimic the behaviour of combustion system instabilities.
$\mu =0.2$ resembles the dimensionless pressure perturbation as shown in figure 1, proving that the classical VDP equation can mimic the behaviour of combustion system instabilities.

Figure 1. Instability of a combustion system obtained (a) experimentally (Li et al. Reference Li, Li, Tang, Yang, Fu, Clarke, Jin, Ji and Zhao2016a) and (b) with the classical VDP equation.
To enhance the applicability of the classical VDP equation to thermoacoustic instabilities, we decompose the first-order differential term and add a time scaling parameter ![]() $\mu _3$ to reformulate (2.1) into
$\mu _3$ to reformulate (2.1) into
Equation (2.2) still satisfies the properties of the Liénard theorem, providing a unique and stable limit cycle. Observing the shape of the oscillation depicted in figure 1, the fundamental characteristics are the time required for the initial perturbation to evolve into a limit cycle, and the resulting limit cycle amplitude. Figure 2 visualizes the extension of the parameter space, introducing further parameters, thereby improving the expressive capacity compared to the one-dimensional diagonal line (![]() $\mu _1=\mu _2$).
$\mu _1=\mu _2$).

Figure 2. Contour plots of (a) the limit cycle amplitude (![]() $A_{lc}$), and (b) the time duration to reach a limit cycle (
$A_{lc}$), and (b) the time duration to reach a limit cycle (![]() $\Delta t_{lc}$, where the value zero indicates an unexcited oscillator).
$\Delta t_{lc}$, where the value zero indicates an unexcited oscillator).
To further characterize the dynamics described in (2.2), the Krylov–Bogolyubov method of averaging is applied (Krylov & Bogolyubov Reference Krylov and Bogolyubov1947; Nayfeh Reference Nayfeh2000). Therefore, (2.2) is rewritten as
Here, ![]() $\varepsilon _a$ is introduced as a placeholder with a small value to facilitate the averaging procedure. Making this assumption implies weak nonlinearity (small
$\varepsilon _a$ is introduced as a placeholder with a small value to facilitate the averaging procedure. Making this assumption implies weak nonlinearity (small ![]() $\mu _1$ and
$\mu _1$ and ![]() $\mu _2$), causing the oscillator to behave as one undergoing sinusoidal oscillations, which is common for thermoacoustic applications. Therefore, this solution is valid only in the region where
$\mu _2$), causing the oscillator to behave as one undergoing sinusoidal oscillations, which is common for thermoacoustic applications. Therefore, this solution is valid only in the region where ![]() $\mu _1$ and
$\mu _1$ and ![]() $\mu _2$ are small, a condition utilized throughout this paper. In fact, setting
$\mu _2$ are small, a condition utilized throughout this paper. In fact, setting ![]() $\mu _1 = \mu _2 = \varepsilon _a$ and
$\mu _1 = \mu _2 = \varepsilon _a$ and ![]() $\mu _3 = 1$ recovers the classical VDP oscillator. Proceeding, the solution is assumed to have the form
$\mu _3 = 1$ recovers the classical VDP oscillator. Proceeding, the solution is assumed to have the form
where ![]() $a(t)$ and
$a(t)$ and ![]() $\theta (t)$ are time-varying. However, they vary slowly compared to the period of oscillations due to the assumption made previously on
$\theta (t)$ are time-varying. However, they vary slowly compared to the period of oscillations due to the assumption made previously on ![]() $\varepsilon _a$ in (2.3). This leads to the following two equations for the amplitude and phase responses, respectively:
$\varepsilon _a$ in (2.3). This leads to the following two equations for the amplitude and phase responses, respectively:
and
where ![]() $F(a)$ and
$F(a)$ and ![]() $G(a)$ represent coefficients of the Fourier expansion of the right-hand side of (2.3). They can be expressed as
$G(a)$ represent coefficients of the Fourier expansion of the right-hand side of (2.3). They can be expressed as
and
As a result, the phase remains constant, and the amplitude is further described as
 \begin{equation} a(t) = \frac{2
\exp({\tfrac12\varepsilon_a \mu_1 \mu_3 t})
\sqrt{\mu_1}}{\sqrt{\dfrac{4 \mu_1}{a_0^2} + \mu_2
\bigl(\exp({\varepsilon_a \mu_1 \mu_3 t}) - 1\bigr)}},
\end{equation}
\begin{equation} a(t) = \frac{2
\exp({\tfrac12\varepsilon_a \mu_1 \mu_3 t})
\sqrt{\mu_1}}{\sqrt{\dfrac{4 \mu_1}{a_0^2} + \mu_2
\bigl(\exp({\varepsilon_a \mu_1 \mu_3 t}) - 1\bigr)}},
\end{equation}
with the initial condition ![]() $a(0) = a_0$ already included. Using this equation for amplitude, we find the limit cycle oscillation as
$a(0) = a_0$ already included. Using this equation for amplitude, we find the limit cycle oscillation as
This formulation has a remarkable resemblance to figure 2. It is apparent that a strong agreement with the numerical integration of (2.2) is obtained.
2.1.1. The PINNs model for inverting a thermoacoustic oscillations problem
Estimating unknown variables based on the experimental measurements or available data from theoretical models constitutes a typical inverse problem. Therefore, the PINNs algorithm for solving inverse problems is highly suitable for addressing this system generalization task, as outlined in figure 3. Here, the integration of PDEs and available data is accomplished seamlessly by incorporating new PDE loss terms into the loss function of the neural network (Yazdani et al. Reference Yazdani, Lu, Raissi and Karniadakis2020; Karniadakis et al. Reference Karniadakis, Kevrekidis, Lu, Perdikaris, Wang and Yang2021; Yu et al. Reference Yu, Lu, Meng and Karniadakis2022). As depicted in (2.11) below, the total loss consists of the supervised data loss and unsupervised PDEs loss (EVDP equation here):
where
 $$\begin{gather} L_{data}=\frac{1}{N_{data}}\sum^{N_{data}}_{i=1}\left[\psi(t_{i},\boldsymbol{\mu})-\psi(t_{i})\right]^2, \end{gather}$$
$$\begin{gather} L_{data}=\frac{1}{N_{data}}\sum^{N_{data}}_{i=1}\left[\psi(t_{i},\boldsymbol{\mu})-\psi(t_{i})\right]^2, \end{gather}$$ $$\begin{gather}L_{PDE}= \frac{1}{N_{data}}\sum^{N_{data}}_{j=1}\left[\ddot{\psi}(t_j)-\mu_1\mu_3\, \dot{\psi}(t_j)+\mu_2\mu_3\,\psi^2(t_j)\,\dot{\psi}(t_j)+\mu_3^2\,\psi(t_j)\right]^2. \end{gather}$$
$$\begin{gather}L_{PDE}= \frac{1}{N_{data}}\sum^{N_{data}}_{j=1}\left[\ddot{\psi}(t_j)-\mu_1\mu_3\, \dot{\psi}(t_j)+\mu_2\mu_3\,\psi^2(t_j)\,\dot{\psi}(t_j)+\mu_3^2\,\psi(t_j)\right]^2. \end{gather}$$
Here, ![]() $\omega _{data}$ and
$\omega _{data}$ and ![]() $\omega _{PDE}$ are the loss weights of the supervised loss
$\omega _{PDE}$ are the loss weights of the supervised loss ![]() $L_{data}$ and the unsupervised PDE loss
$L_{data}$ and the unsupervised PDE loss ![]() $L_{PDE}$, respectively,
$L_{PDE}$, respectively, ![]() $N_{data}$ represents the number of the training data, and
$N_{data}$ represents the number of the training data, and ![]() $\psi (t_i)$ and
$\psi (t_i)$ and ![]() $\psi (t_i, \boldsymbol{\mu})$ are the
$\psi (t_i, \boldsymbol{\mu})$ are the ![]() $i$th training node and its fitting value.
$i$th training node and its fitting value.

Figure 3. The PINNs architecture for the inverse thermoacoustic problem. Here, ![]() $MSE_{data}$ and
$MSE_{data}$ and ![]() $MSE_{PDE}$ represent the mean square error of the data and the PDE, respectively.
$MSE_{PDE}$ represent the mean square error of the data and the PDE, respectively.
The neural network parameters and unknowns, ![]() $\boldsymbol {\mu }$ can be determined simultaneously by minimizing the loss function
$\boldsymbol {\mu }$ can be determined simultaneously by minimizing the loss function ![]() $L$ through a gradient-based optimizer (the Adam optimizer was applied in the present work). In the features layer, employing
$L$ through a gradient-based optimizer (the Adam optimizer was applied in the present work). In the features layer, employing ![]() $m$ functions of the form
$m$ functions of the form ![]() $e(\cdot )$ to construct
$e(\cdot )$ to construct ![]() $m$ features
$m$ features ![]() $e(t)$ for specific solution patterns of the PDEs is efficient. Trigonometric functions are used due to the oscillation periodicity in this study. The training is performed using all the data (including the exponentially growing period and the saturating period) with default hyperparameters and learning rate
$e(t)$ for specific solution patterns of the PDEs is efficient. Trigonometric functions are used due to the oscillation periodicity in this study. The training is performed using all the data (including the exponentially growing period and the saturating period) with default hyperparameters and learning rate ![]() $10^{-3}$. Additionally, a two-stage training strategy is employed to accelerate the network convergence, which involves initial training with only supervised losses, and further training considering all losses. The algorithm is implemented in Python using the open-source library DeepXDE (Lu et al. Reference Lu, Meng, Mao and Karniadakis2021). The unknown variables are acquired when stabilizing with the neural network time step.
$10^{-3}$. Additionally, a two-stage training strategy is employed to accelerate the network convergence, which involves initial training with only supervised losses, and further training considering all losses. The algorithm is implemented in Python using the open-source library DeepXDE (Lu et al. Reference Lu, Meng, Mao and Karniadakis2021). The unknown variables are acquired when stabilizing with the neural network time step.
2.2. Thermoacoustic waves generation and propagation
An analytically traceable system is selected to validate the aforementioned method's effectiveness in obtaining deterministic descriptions. Among various prototypical thermoacoustic systems, the horizontal Rijke tube with acoustically compact heat sources (Rayleigh Reference Rayleigh1878; Raun et al. Reference Raun, Beckstead, Finlinson and Brooks1993) is suitable and considered in this work. The heat release is modelled by the modified King's law theory (Heckl Reference Heckl1990). The dimensionless governing equations are
 $$\begin{gather}\frac{\partial
p}{\partial t}+\frac{\partial u}{\partial x}+\zeta
p-\beta\biggl\{\left|\frac{1}{3}+u_{f}(t-\tau_1)\right|^{{1}/{2}}\biggr\}\delta_D(x-x_{f})=0,
\end{gather}$$
$$\begin{gather}\frac{\partial
p}{\partial t}+\frac{\partial u}{\partial x}+\zeta
p-\beta\biggl\{\left|\frac{1}{3}+u_{f}(t-\tau_1)\right|^{{1}/{2}}\biggr\}\delta_D(x-x_{f})=0,
\end{gather}$$
where the flow parameters ![]() $u$,
$u$, ![]() $p$ and
$p$ and ![]() $\rho$ represent the fluctuation components of velocity, pressure and density, respectively. Here,
$\rho$ represent the fluctuation components of velocity, pressure and density, respectively. Here, ![]() $\zeta$ is a damping coefficient,
$\zeta$ is a damping coefficient, ![]() $\tau _1$ is a time delay between the velocity preoccupation and the heat source response,
$\tau _1$ is a time delay between the velocity preoccupation and the heat source response, ![]() $x_f$ is the location of the hot wire, and
$x_f$ is the location of the hot wire, and ![]() $\delta _D$ is the Kronecker delta. Also,
$\delta _D$ is the Kronecker delta. Also, ![]() $\beta$ is the dimensionless heater power containing all hot-wire parameters:
$\beta$ is the dimensionless heater power containing all hot-wire parameters:
 \begin{equation} \beta=\frac{1}{p_0\sqrt{u_0}}\,\frac{\gamma-1}{\gamma}\,\frac{2L_{w}(T_{w}-T_0)}{S\sqrt{3}} \left({\rm \pi}\lambda_0c_{v}\rho_0\,\frac{d_{w}}{2}\right)^{1/2}, \end{equation}
\begin{equation} \beta=\frac{1}{p_0\sqrt{u_0}}\,\frac{\gamma-1}{\gamma}\,\frac{2L_{w}(T_{w}-T_0)}{S\sqrt{3}} \left({\rm \pi}\lambda_0c_{v}\rho_0\,\frac{d_{w}}{2}\right)^{1/2}, \end{equation}
where ![]() $L_{w}$,
$L_{w}$, ![]() $d_{w}$ and
$d_{w}$ and ![]() $T_{w}$ represent the length, diameter and temperature of the hot wire, respectively. Here,
$T_{w}$ represent the length, diameter and temperature of the hot wire, respectively. Here, ![]() $S$ is the cross-sectional area of the Rijke tube,
$S$ is the cross-sectional area of the Rijke tube, ![]() $\lambda _0$ is the heat conductivity,
$\lambda _0$ is the heat conductivity, ![]() $c_v$ is the specific isochoric heat capacity, and
$c_v$ is the specific isochoric heat capacity, and ![]() $\rho _0$,
$\rho _0$, ![]() $p_0$,
$p_0$, ![]() $u_0$ and
$u_0$ and ![]() $T_0$ are the density, pressure, velocity and temperature at the inlet.
$T_0$ are the density, pressure, velocity and temperature at the inlet.
Substituting the pressure perturbations expanded as a Galerkin series (Nagaraja, Kedia & Sujith Reference Nagaraja, Kedia and Sujith2009; Juniper Reference Juniper2011) into (2.14) gives
 $$\begin{gather} p=\sum_{n=1}^N\dot{\eta}_n(t)\,\varphi_n(x), \end{gather}$$
$$\begin{gather} p=\sum_{n=1}^N\dot{\eta}_n(t)\,\varphi_n(x), \end{gather}$$ $$\begin{gather}u={-}\sum_{n=1}^N\eta_n(t)\,\varphi'_n(x), \end{gather}$$
$$\begin{gather}u={-}\sum_{n=1}^N\eta_n(t)\,\varphi'_n(x), \end{gather}$$
where ![]() $N$ denotes the mode number, the overdot denotes the time derivative, the prime denotes the spatial derivative, and the functions
$N$ denotes the mode number, the overdot denotes the time derivative, the prime denotes the spatial derivative, and the functions ![]() $\varphi _n(x)$ are the eigensolutions of the homogeneous wave equation for the Rijke tube. Because the Rijke tube has pressure nodes at both ends, the mode shapes
$\varphi _n(x)$ are the eigensolutions of the homogeneous wave equation for the Rijke tube. Because the Rijke tube has pressure nodes at both ends, the mode shapes ![]() $\varphi _n(x)$ corresponding to the
$\varphi _n(x)$ corresponding to the ![]() $n$th mode are illustrated as
$n$th mode are illustrated as
 \begin{equation} \varphi_n(x)=\left\{\begin{array}{ll} \sin\left(\dfrac{\omega_nL}{\bar{c}_1}\,x\right), & x\in[0,x_f], \\[10pt] \dfrac{\sin\left(\dfrac{\omega_nL}{\bar{c}_1}\,x_f\right)}{\sin\left(\dfrac{\omega_{n}L}{\bar{c}_2}\,x_f\right)} \sin\left[\dfrac{\omega_nL}{\bar{c}_2}\,(1-x)\right], & x\in [x_f,1], \end{array} \right. \end{equation}
\begin{equation} \varphi_n(x)=\left\{\begin{array}{ll} \sin\left(\dfrac{\omega_nL}{\bar{c}_1}\,x\right), & x\in[0,x_f], \\[10pt] \dfrac{\sin\left(\dfrac{\omega_nL}{\bar{c}_1}\,x_f\right)}{\sin\left(\dfrac{\omega_{n}L}{\bar{c}_2}\,x_f\right)} \sin\left[\dfrac{\omega_nL}{\bar{c}_2}\,(1-x)\right], & x\in [x_f,1], \end{array} \right. \end{equation}
which satisfy the orthogonality condition. Here, ![]() $L$ is the length of the Rijke tube, and
$L$ is the length of the Rijke tube, and ![]() $\bar {c}_1$ and
$\bar {c}_1$ and ![]() $\bar {c}_2$ are the speed of sound upstream and downstream of the hot wire. Substituting the Galerkin expansion into (2.14) and (2.15) leads to
$\bar {c}_2$ are the speed of sound upstream and downstream of the hot wire. Substituting the Galerkin expansion into (2.14) and (2.15) leads to
 \begin{align} \frac{\mathrm{d}\dot{\eta}_n(t)}{\mathrm{d}t}+(\omega_n)^2\,\eta_n(t)+\zeta_n\, \dot{\eta}_n(t)=\frac{\beta}{E_n}\varphi_n(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'_n(x_{f})\, \eta_n(t-\tau_1)\right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}, \end{align}
\begin{align} \frac{\mathrm{d}\dot{\eta}_n(t)}{\mathrm{d}t}+(\omega_n)^2\,\eta_n(t)+\zeta_n\, \dot{\eta}_n(t)=\frac{\beta}{E_n}\varphi_n(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'_n(x_{f})\, \eta_n(t-\tau_1)\right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}, \end{align}
where ![]() $\omega _n$ are the eigenfrequencies calculated from the pressure and velocity continuity over the heat source (Backhaus & Swift Reference Backhaus and Swift1999; Zhao & Reyhanoglu Reference Zhao and Reyhanoglu2014; Karniadakis et al. Reference Karniadakis, Kevrekidis, Lu, Perdikaris, Wang and Yang2021),
$\omega _n$ are the eigenfrequencies calculated from the pressure and velocity continuity over the heat source (Backhaus & Swift Reference Backhaus and Swift1999; Zhao & Reyhanoglu Reference Zhao and Reyhanoglu2014; Karniadakis et al. Reference Karniadakis, Kevrekidis, Lu, Perdikaris, Wang and Yang2021), ![]() $E_n$ are the integral constants (refer to the condition of orthogonality that is described mathematically in (32) of the previous work, Zhao Reference Zhao2012), and
$E_n$ are the integral constants (refer to the condition of orthogonality that is described mathematically in (32) of the previous work, Zhao Reference Zhao2012), and ![]() $\zeta _n$ are the damping coefficients (Nagaraja et al. Reference Nagaraja, Kedia and Sujith2009; Li et al. Reference Li, Zhao, Yang, Wen, Jin, Li, Zhao, Xie and Liu2016b), accounting for all damping effects such as energy losses due to radiation, or viscous dissipation. The damping coefficient can be related to the eigenfrequency by
$\zeta _n$ are the damping coefficients (Nagaraja et al. Reference Nagaraja, Kedia and Sujith2009; Li et al. Reference Li, Zhao, Yang, Wen, Jin, Li, Zhao, Xie and Liu2016b), accounting for all damping effects such as energy losses due to radiation, or viscous dissipation. The damping coefficient can be related to the eigenfrequency by
where ![]() $\xi _1$ and
$\xi _1$ and ![]() $\xi _2$ account for the energy losses due to radiation at the open ends as well as dissipation within the acoustic viscous and thermal boundary layers at the walls.
$\xi _2$ account for the energy losses due to radiation at the open ends as well as dissipation within the acoustic viscous and thermal boundary layers at the walls.
According to Bonciolini et al. (Reference Bonciolini, Faure-Beaulieu, Bourquard and Noiray2021), only one dominant eigenmode is needed to approximate the system stability, including the limit cycle, although the unstable modes are coupled via nonlinear heat release rates. Thus the one-mode Galerkin expansion is employed in this study. The thermoacoustic Rijke tube system is represented by the coefficient values selected from previous studies (Backhaus & Swift Reference Backhaus and Swift1999; Balasubramanian & Sujith Reference Balasubramanian and Sujith2008), which are listed in Appendix B. The initial conditions ![]() $[\eta (0), \eta '(0)]$ are assigned randomly, and kept consistent for the theoretical Rijke tube and EVDP system. As shown in figure 4, the system oscillations in terms of
$[\eta (0), \eta '(0)]$ are assigned randomly, and kept consistent for the theoretical Rijke tube and EVDP system. As shown in figure 4, the system oscillations in terms of ![]() $\eta (t)$ and
$\eta (t)$ and ![]() $\dot {\eta }(t)$ decay with low heater power or are excited to limit cycles (triggering) with high heater power. The Hopf bifurcation diagram in figure 4(a) shows that the limit cycle amplitude of the system behaves asymptotically as a function of
$\dot {\eta }(t)$ decay with low heater power or are excited to limit cycles (triggering) with high heater power. The Hopf bifurcation diagram in figure 4(a) shows that the limit cycle amplitude of the system behaves asymptotically as a function of ![]() $\beta$. Crossing the Hopf point (
$\beta$. Crossing the Hopf point (![]() $\beta _{Hopf}=1.17$) through the forward path, the system undergoes a Hopf bifurcation, which leads to an amplitude rise. In the reverse path,
$\beta _{Hopf}=1.17$) through the forward path, the system undergoes a Hopf bifurcation, which leads to an amplitude rise. In the reverse path, ![]() $\beta$ needs to be decreased significantly below the Hopf point to return the system to a stable state (known as the saddle point (
$\beta$ needs to be decreased significantly below the Hopf point to return the system to a stable state (known as the saddle point (![]() $\beta _{saddle}=1.01$). A typical subcritical bifurcation with a hysteresis region (bistable region) (Subramanian, Sujith & Wahi Reference Subramanian, Sujith and Wahi2013; Biwa et al. Reference Biwa, Tozuka and Yazaki2015) is observed. In this region, the system can exhibit either a fixed stable point or a stable limit cycle, depending on the initial perturbations (Sujith & Unni Reference Sujith and Unni2020; Liu et al. Reference Liu, Liu, Wang, Ao and Guan2023). These interpretations are consistent with previous studies (Thomas et al. Reference Thomas, Mondal, Pawar and Sujith2018), indicating that the theoretical Rijke tube model generates reliable input data for the PINNs model to fit the unknown parameters of the EVDP equation.
$\beta _{saddle}=1.01$). A typical subcritical bifurcation with a hysteresis region (bistable region) (Subramanian, Sujith & Wahi Reference Subramanian, Sujith and Wahi2013; Biwa et al. Reference Biwa, Tozuka and Yazaki2015) is observed. In this region, the system can exhibit either a fixed stable point or a stable limit cycle, depending on the initial perturbations (Sujith & Unni Reference Sujith and Unni2020; Liu et al. Reference Liu, Liu, Wang, Ao and Guan2023). These interpretations are consistent with previous studies (Thomas et al. Reference Thomas, Mondal, Pawar and Sujith2018), indicating that the theoretical Rijke tube model generates reliable input data for the PINNs model to fit the unknown parameters of the EVDP equation.

Figure 4. Rijke tube system. (a) Subcritical bifurcation diagram of the limit cycle amplitudes versus ![]() $\beta$. (b) Unexcited oscillation with small
$\beta$. (b) Unexcited oscillation with small ![]() $\beta =0.5$, AD – the amplitude tends to zero with time. (c) Excited oscillation with large
$\beta =0.5$, AD – the amplitude tends to zero with time. (c) Excited oscillation with large ![]() $\beta =2.1$, limit cycle oscillation – the amplitude tends to a non-zero stable value with time.
$\beta =2.1$, limit cycle oscillation – the amplitude tends to a non-zero stable value with time.
Equation (2.20) can be rewritten for the first mode:
 \begin{equation}
\frac{\mathrm{d}^2
\eta(t)}{\mathrm{d} t^2} + \frac{\bar{\zeta}
\omega}{\rm \pi}\,\dot{\eta}(t) + \omega^2\,\eta(t) =
\frac{\beta}{E}\,\varphi(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'(x_{f})\,\eta
(t-\tau_1)\right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}.
\end{equation}
\begin{equation}
\frac{\mathrm{d}^2
\eta(t)}{\mathrm{d} t^2} + \frac{\bar{\zeta}
\omega}{\rm \pi}\,\dot{\eta}(t) + \omega^2\,\eta(t) =
\frac{\beta}{E}\,\varphi(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'(x_{f})\,\eta
(t-\tau_1)\right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}.
\end{equation}
An approximate solution may be found by applying the generalized scaling method (Nayfeh Reference Nayfeh2000). This method, related to the multiple scales technique, allows examination of both the amplitude response and the time scales of the problem. A small scaling parameter ![]() $\varepsilon = 1 / \omega$ is inserted into (2.20):
$\varepsilon = 1 / \omega$ is inserted into (2.20):
 \begin{align} \varepsilon^2\,\frac{\mathrm{d}^2 \eta(t)}{\mathrm{d} t^2} + \varepsilon\,\frac{\bar{\zeta} }{\rm \pi}\, \dot{\eta}(t) + \eta(t) = \varepsilon^2\, \frac{\beta}{E}\,\varphi(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'(x_{f})\,\eta(t-\tau_1) \right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}. \end{align}
\begin{align} \varepsilon^2\,\frac{\mathrm{d}^2 \eta(t)}{\mathrm{d} t^2} + \varepsilon\,\frac{\bar{\zeta} }{\rm \pi}\, \dot{\eta}(t) + \eta(t) = \varepsilon^2\, \frac{\beta}{E}\,\varphi(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'(x_{f})\,\eta(t-\tau_1) \right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}. \end{align}Although an approximate solution can be derived, it is quite cumbersome. Substituting the heat release term with an alternative formulation (Zhao et al. Reference Zhao, Zhao, Cheng, Shelton and Majdalani2023) leads to
where ![]() $K$ is the heat correlation strength parameter. A time scale expansion is introduced with a slow and a fast time scale to aid the understanding of the underlying physics:
$K$ is the heat correlation strength parameter. A time scale expansion is introduced with a slow and a fast time scale to aid the understanding of the underlying physics:
where ![]() $g_i$ will be determined through solvability conditions during the analysis. The temporal derivatives are also expanded:
$g_i$ will be determined through solvability conditions during the analysis. The temporal derivatives are also expanded:
and
 \begin{align} \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{t^2}}}&= \frac{{{\partial ^2}}}{{\partial t_0^2}} + 2 \left( {\frac{{{{g_0'}}}}{\varepsilon } + {{g_1'}} + \varepsilon {{g_2'}} + \cdots} \right)\frac{{{\partial ^2}}}{{\partial {t_0}\,\partial {t_1}}} \nonumber\\ &\quad + \left( {\frac{{{{g_0''}}}}{\varepsilon } + {{g_1''}} + \varepsilon {{g_2''}} + \cdots} \right)\frac{\partial }{{\partial {t_1}}} + {\left( {\frac{{{{g_0'}}}}{\varepsilon } + {{g_1'}} + \varepsilon {{g_2'}} + \cdots} \right)^2}\frac{{{\partial ^2}}}{{\partial t_1^2}}. \end{align}
\begin{align} \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{t^2}}}&= \frac{{{\partial ^2}}}{{\partial t_0^2}} + 2 \left( {\frac{{{{g_0'}}}}{\varepsilon } + {{g_1'}} + \varepsilon {{g_2'}} + \cdots} \right)\frac{{{\partial ^2}}}{{\partial {t_0}\,\partial {t_1}}} \nonumber\\ &\quad + \left( {\frac{{{{g_0''}}}}{\varepsilon } + {{g_1''}} + \varepsilon {{g_2''}} + \cdots} \right)\frac{\partial }{{\partial {t_1}}} + {\left( {\frac{{{{g_0'}}}}{\varepsilon } + {{g_1'}} + \varepsilon {{g_2'}} + \cdots} \right)^2}\frac{{{\partial ^2}}}{{\partial t_1^2}}. \end{align}
Also, the time-varying coefficient ![]() $\eta$ can be expanded as a function of the two coordinates:
$\eta$ can be expanded as a function of the two coordinates:
Therefore, an approximate solution may be achieved with the relevant slow and fast time scale separation, which will aid in the understanding of the physics present. The three equations at different orders to be solved are given as
for the leading order,
 \begin{align} &\left(g_0'\right)^2 \frac{\partial^2 \eta_1 }{\partial t_1^2} + \frac{\bar{\zeta}}{\rm \pi}\,g_0'\, \frac{\partial \eta_1}{\partial t_1} + \eta_1 + K \tau_1\,\varphi(x_{f})\, \varphi'(x_{f})\,g_0'\,\frac{\partial \eta_0}{\partial t_1} \nonumber\\ &\quad + \frac{\bar{\zeta} g_1'}{\rm \pi}\,\frac{\partial \eta_0}{\partial t_1} + g_0''\,\frac{\partial \eta_0}{\partial t_1} + 2 g_0' g_1'\,\frac{\partial^2 \eta_0}{\partial t_1^2} + \frac{\bar{\zeta}}{\rm \pi}\,\frac{\partial \eta_0}{\partial t_0} + 2 g_0'\,\frac{\partial^2 \eta_0}{\partial t_1\,\partial t_0} = 0 \end{align}
\begin{align} &\left(g_0'\right)^2 \frac{\partial^2 \eta_1 }{\partial t_1^2} + \frac{\bar{\zeta}}{\rm \pi}\,g_0'\, \frac{\partial \eta_1}{\partial t_1} + \eta_1 + K \tau_1\,\varphi(x_{f})\, \varphi'(x_{f})\,g_0'\,\frac{\partial \eta_0}{\partial t_1} \nonumber\\ &\quad + \frac{\bar{\zeta} g_1'}{\rm \pi}\,\frac{\partial \eta_0}{\partial t_1} + g_0''\,\frac{\partial \eta_0}{\partial t_1} + 2 g_0' g_1'\,\frac{\partial^2 \eta_0}{\partial t_1^2} + \frac{\bar{\zeta}}{\rm \pi}\,\frac{\partial \eta_0}{\partial t_0} + 2 g_0'\,\frac{\partial^2 \eta_0}{\partial t_1\,\partial t_0} = 0 \end{align}for the first order, and
 \begin{align} &\left(g_0'\right)^2
\frac{\partial^2 \eta_2 }{\partial t_1^2} +
\frac{\bar{\zeta}}{\rm \pi}\,g_0'\, \frac{\partial
\eta_2}{\partial t_1} + \eta_2 -
K\,\varphi(x_{f})\,\varphi'(x_{f})\, \eta_0 +
\frac{\bar{\zeta} g_2'}{\rm \pi}\,\frac{\partial
\eta_0}{\partial t_1}+ K \tau_1\,
\varphi(x_{f})\,\varphi'(x_{f})\,g_1'\,\frac{\partial
\eta_0}{\partial t_1} \nonumber\\
&\quad+ K \tau_1\, \varphi(x_{f})\,\varphi'(x_{f})\,g_0'\,\frac{\partial
\eta_1}{\partial t_1} + g_1''\, \frac{\partial
\eta_0}{\partial t_1} + \frac{\bar{\zeta}
g_1'}{\rm \pi}\,\frac{\partial \eta_1}{\partial t_1} +
g_0''\,\frac{\partial \eta_1}{ \partial t_1} \nonumber\\
&\quad +
\left(g_1'\right)^2 \frac{\partial^2 \eta_0}{\partial
t_1^2} + 2 g_0' g_2'\,\frac{\partial^2 \eta_0}{\partial
t_1^2} + 2 g_0' g_1'\,\frac{\partial^2
\eta_1}{\partial t_1^2} + \frac{\bar{\zeta}}{\rm \pi}\,
\frac{\partial \eta_1}{\partial t_0} + 2
g_1'\,\frac{\partial^2 \eta_0}{\partial
t_1\,\partial t_0}\nonumber\\
&\quad + 2 g_0'\,\frac{\partial^2
\eta_1 }{\partial t_1\,\partial t_0} + \frac{\partial^2
\eta_0}{\partial t_0^2} +
K\,\varphi(x_{f})\,\varphi'(x_{f})\,\tau_1\,\frac{\partial \eta_0}{\partial t_0} =
0
\end{align}
\begin{align} &\left(g_0'\right)^2
\frac{\partial^2 \eta_2 }{\partial t_1^2} +
\frac{\bar{\zeta}}{\rm \pi}\,g_0'\, \frac{\partial
\eta_2}{\partial t_1} + \eta_2 -
K\,\varphi(x_{f})\,\varphi'(x_{f})\, \eta_0 +
\frac{\bar{\zeta} g_2'}{\rm \pi}\,\frac{\partial
\eta_0}{\partial t_1}+ K \tau_1\,
\varphi(x_{f})\,\varphi'(x_{f})\,g_1'\,\frac{\partial
\eta_0}{\partial t_1} \nonumber\\
&\quad+ K \tau_1\, \varphi(x_{f})\,\varphi'(x_{f})\,g_0'\,\frac{\partial
\eta_1}{\partial t_1} + g_1''\, \frac{\partial
\eta_0}{\partial t_1} + \frac{\bar{\zeta}
g_1'}{\rm \pi}\,\frac{\partial \eta_1}{\partial t_1} +
g_0''\,\frac{\partial \eta_1}{ \partial t_1} \nonumber\\
&\quad +
\left(g_1'\right)^2 \frac{\partial^2 \eta_0}{\partial
t_1^2} + 2 g_0' g_2'\,\frac{\partial^2 \eta_0}{\partial
t_1^2} + 2 g_0' g_1'\,\frac{\partial^2
\eta_1}{\partial t_1^2} + \frac{\bar{\zeta}}{\rm \pi}\,
\frac{\partial \eta_1}{\partial t_0} + 2
g_1'\,\frac{\partial^2 \eta_0}{\partial
t_1\,\partial t_0}\nonumber\\
&\quad + 2 g_0'\,\frac{\partial^2
\eta_1 }{\partial t_1\,\partial t_0} + \frac{\partial^2
\eta_0}{\partial t_0^2} +
K\,\varphi(x_{f})\,\varphi'(x_{f})\,\tau_1\,\frac{\partial \eta_0}{\partial t_0} =
0
\end{align}for the second order. As is typical with perturbation expansions, the homogeneous part of the equations has a common form, which can be described physically as a damped oscillator. Equation (2.29) may be solved readily as
As (2.30) and (2.31) have the same form as (2.29), the form of the homogeneous solution part should also be the same. Hence
and
The solutions are of eikonal form, which has two roots and is typical for wave propagation. The scales ![]() $g_0$ and
$g_0$ and ![]() $g_1$ along with coefficients
$g_1$ along with coefficients ![]() $A$ and
$A$ and ![]() $B$ can be expressed in closed form from (2.29) and (2.30). To accomplish this, the first scale
$B$ can be expressed in closed form from (2.29) and (2.30). To accomplish this, the first scale ![]() $g_0$ can be solved. Hence the exponential factor may be examined as
$g_0$ can be solved. Hence the exponential factor may be examined as
To ensure a bounded solution, the derivative of ![]() $\gamma (t_0)$ must be zero (Nayfeh Reference Nayfeh2000). Therefore, the following ordinary differential equations (ODEs) are solved:
$\gamma (t_0)$ must be zero (Nayfeh Reference Nayfeh2000). Therefore, the following ordinary differential equations (ODEs) are solved:
where ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _{2}$ are constants. The solutions for the scales can be written as
$\gamma _{2}$ are constants. The solutions for the scales can be written as
To determine the conjugate functions ![]() $A$ and
$A$ and ![]() $B$, the terms corresponding to
$B$, the terms corresponding to ![]() $\exp (\gamma _1 t_1)$ and
$\exp (\gamma _1 t_1)$ and ![]() $\exp (\gamma _2 t_1)$ are gathered and set to zero. Due to this constraint, singularities are suppressed, and two ODEs are obtained for
$\exp (\gamma _2 t_1)$ are gathered and set to zero. Due to this constraint, singularities are suppressed, and two ODEs are obtained for ![]() $A$ and
$A$ and ![]() $B$:
$B$:
 \begin{align} &\frac{\mathrm{d}
A}{\mathrm{d} t_0} \left(\bar{\zeta} + 2 {\rm \pi}\gamma_1
g_{0,1}'\right) + \left[{\rm \pi} + \gamma_1 g_{0,1}'
\left(\bar{\zeta} + {\rm \pi}\gamma_1 g_{0,1}'\right)\right]
C(t_0) \nonumber\\ &\quad +\big\{ 2{\rm \pi} \gamma_1^2
g_{0,1}' g_{1,1}' + \gamma_1 \left[\zeta g_{1,1}' + {\rm \pi}
\left(g_{0,1}' \left(K
\tau_1\,\varphi(x_{f})\,\varphi'(x_{f}) \right) +
g_{0,1}''\right)\right]\big\} A(t_0) = 0
\end{align}
\begin{align} &\frac{\mathrm{d}
A}{\mathrm{d} t_0} \left(\bar{\zeta} + 2 {\rm \pi}\gamma_1
g_{0,1}'\right) + \left[{\rm \pi} + \gamma_1 g_{0,1}'
\left(\bar{\zeta} + {\rm \pi}\gamma_1 g_{0,1}'\right)\right]
C(t_0) \nonumber\\ &\quad +\big\{ 2{\rm \pi} \gamma_1^2
g_{0,1}' g_{1,1}' + \gamma_1 \left[\zeta g_{1,1}' + {\rm \pi}
\left(g_{0,1}' \left(K
\tau_1\,\varphi(x_{f})\,\varphi'(x_{f}) \right) +
g_{0,1}''\right)\right]\big\} A(t_0) = 0
\end{align}
and
 \begin{align} &\frac{\mathrm{d}
B}{\mathrm{d} t_0} \left(\bar{\zeta} + 2 {\rm \pi}\gamma_2
g_{0,2}'\right) + \left[{\rm \pi} + \gamma_2 g_{0,2}'
\left(\bar{\zeta} + {\rm \pi}\gamma_2 g_{0,2}'\right)\right]
D(t_0) \nonumber\\ &\quad+ \big\{ 2 {\rm \pi}\gamma_2^2
g_{0,2}' g_{1,2}' + \gamma_2 \left[\zeta g_{1,2}' + {\rm \pi}
\left(g_{0,2}' \left(K \tau_1\,\varphi(x_{f})\,\varphi'(x_{f}) \right) +
g_{0,2}''\right)\right]\big\} B(t_0) = 0.
\end{align}
\begin{align} &\frac{\mathrm{d}
B}{\mathrm{d} t_0} \left(\bar{\zeta} + 2 {\rm \pi}\gamma_2
g_{0,2}'\right) + \left[{\rm \pi} + \gamma_2 g_{0,2}'
\left(\bar{\zeta} + {\rm \pi}\gamma_2 g_{0,2}'\right)\right]
D(t_0) \nonumber\\ &\quad+ \big\{ 2 {\rm \pi}\gamma_2^2
g_{0,2}' g_{1,2}' + \gamma_2 \left[\zeta g_{1,2}' + {\rm \pi}
\left(g_{0,2}' \left(K \tau_1\,\varphi(x_{f})\,\varphi'(x_{f}) \right) +
g_{0,2}''\right)\right]\big\} B(t_0) = 0.
\end{align}
The solutions can be written as
 \begin{equation} \left.\begin{gathered}
A(t_0) = a_0 \exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr) \tau_1\,\varphi(x_{f})\,
\varphi'(x_{f}) -
g_{1,1}(t_0)}\biggr),\\ B(t_0) = b_0
\exp\biggl({\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})-
g_{1,2}(t_0)}\biggr).
\end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered}
A(t_0) = a_0 \exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr) \tau_1\,\varphi(x_{f})\,
\varphi'(x_{f}) -
g_{1,1}(t_0)}\biggr),\\ B(t_0) = b_0
\exp\biggl({\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})-
g_{1,2}(t_0)}\biggr).
\end{gathered}\right\}\end{equation}
The first-order scale ![]() $g_1$ appears in both coefficients. The scale may be set to zero without loss of generality as it disappears from the expansion regardless of its value (Nayfeh Reference Nayfeh2000). The natural cancellation of this scale prevents interaction and overlapping scales with regard to
$g_1$ appears in both coefficients. The scale may be set to zero without loss of generality as it disappears from the expansion regardless of its value (Nayfeh Reference Nayfeh2000). The natural cancellation of this scale prevents interaction and overlapping scales with regard to ![]() $t_0$. From this specification, (2.29) and (2.30) are solved completely. The solution of (2.31) provides the coefficients
$t_0$. From this specification, (2.29) and (2.30) are solved completely. The solution of (2.31) provides the coefficients ![]() $C$ and
$C$ and ![]() $D$, along with the slow scale
$D$, along with the slow scale ![]() $g_2$. First, the terms corresponding to
$g_2$. First, the terms corresponding to ![]() $\exp (\gamma _1 t_1)$ and
$\exp (\gamma _1 t_1)$ and ![]() $\exp (\gamma _2 t_1)$ are gathered and set to zero to suppress any singularity behaviour. The ODE for
$\exp (\gamma _2 t_1)$ are gathered and set to zero to suppress any singularity behaviour. The ODE for ![]() $C$ is
$C$ is
 \begin{align} &\frac{\mathrm{d}
C}{\mathrm{d} t_0} + \frac{\{ E(t_0)
[{\rm \pi} + \gamma_1 g_{0,1}' (\bar{\zeta} + {\rm \pi}
\gamma_1 g_{0,1}')] + {\rm \pi}\gamma_1\,C(t_0)
[K \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})\,g_{0,1}' +
g_{0,1}'']\}} {(\bar{\zeta} + 2 {\rm \pi}
\gamma_1 g_{0,1}' )} \nonumber\\ &\quad - [a_0 K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) ({\rm \pi}^2 (4
+ K \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f})) -
\bar{\zeta}^2)\nonumber\\ &\quad - a_0 \gamma_1 (4 {\rm \pi}^2 - \bar{\zeta}^2)
(\bar{\zeta} + 2 {\rm \pi}\gamma_1 g_{0,1}')
g_{2,1}'] \nonumber\\ &\quad \times \frac{1}{(4
{\rm \pi}^2 - \bar{\zeta}^2)(\bar{\zeta} + 2 {\rm \pi}
\gamma_1 g_{0,1}' )} \exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} + 1\biggr)
\tau_1\,\varphi(x_{f})\,\varphi'(x_{f})}\biggr) =
0,
\end{align}
\begin{align} &\frac{\mathrm{d}
C}{\mathrm{d} t_0} + \frac{\{ E(t_0)
[{\rm \pi} + \gamma_1 g_{0,1}' (\bar{\zeta} + {\rm \pi}
\gamma_1 g_{0,1}')] + {\rm \pi}\gamma_1\,C(t_0)
[K \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})\,g_{0,1}' +
g_{0,1}'']\}} {(\bar{\zeta} + 2 {\rm \pi}
\gamma_1 g_{0,1}' )} \nonumber\\ &\quad - [a_0 K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) ({\rm \pi}^2 (4
+ K \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f})) -
\bar{\zeta}^2)\nonumber\\ &\quad - a_0 \gamma_1 (4 {\rm \pi}^2 - \bar{\zeta}^2)
(\bar{\zeta} + 2 {\rm \pi}\gamma_1 g_{0,1}')
g_{2,1}'] \nonumber\\ &\quad \times \frac{1}{(4
{\rm \pi}^2 - \bar{\zeta}^2)(\bar{\zeta} + 2 {\rm \pi}
\gamma_1 g_{0,1}' )} \exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} + 1\biggr)
\tau_1\,\varphi(x_{f})\,\varphi'(x_{f})}\biggr) =
0,
\end{align}
with ![]() $D$ having a similar formulation. The solution can be written as
$D$ having a similar formulation. The solution can be written as
 \begin{align} C(t_0) &= c_0
\exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr) \tau_1\,\varphi(x_{f})\, \varphi'(x_{f})}\biggr)\nonumber\\ &\quad +
\exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})}\biggr)
\nonumber\\ &\quad \times \biggl[\frac{a_0 K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left({\rm \pi}^2 \left(4
+ K \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f})\right) -
\bar{\zeta}^2\right)}{\left(\bar{\zeta}^2 - 4
{\rm \pi}^2\right)^{3/2}}\,t_0 - a_0 \gamma_1 g_{2,1}\biggr]
\end{align}
\begin{align} C(t_0) &= c_0
\exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr) \tau_1\,\varphi(x_{f})\, \varphi'(x_{f})}\biggr)\nonumber\\ &\quad +
\exp\biggl({-\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})}\biggr)
\nonumber\\ &\quad \times \biggl[\frac{a_0 K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left({\rm \pi}^2 \left(4
+ K \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f})\right) -
\bar{\zeta}^2\right)}{\left(\bar{\zeta}^2 - 4
{\rm \pi}^2\right)^{3/2}}\,t_0 - a_0 \gamma_1 g_{2,1}\biggr]
\end{align}
and
 \begin{align}
D(t_0) &= d_0 \exp\biggl({\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})}\biggr)
\nonumber\\ &\quad + \exp\biggl({\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\, \varphi'(x_{f})}
\biggr)\nonumber\\ &\quad \times \biggl[-\frac{b_0 K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) ({\rm \pi}^2 (4
+ K \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f})) -
\bar{\zeta}^2)}{(\bar{\zeta}^2 - 4
{\rm \pi}^2)^{3/2}}\,t_0 - b_0 \gamma_2 g_{2,2}\biggr].
\end{align}
\begin{align}
D(t_0) &= d_0 \exp\biggl({\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f})}\biggr)
\nonumber\\ &\quad + \exp\biggl({\frac{1}{2}\,K t_0
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\, \varphi'(x_{f})}
\biggr)\nonumber\\ &\quad \times \biggl[-\frac{b_0 K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) ({\rm \pi}^2 (4
+ K \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f})) -
\bar{\zeta}^2)}{(\bar{\zeta}^2 - 4
{\rm \pi}^2)^{3/2}}\,t_0 - b_0 \gamma_2 g_{2,2}\biggr].
\end{align}
The slow scale can be solved by eliminating the last part of the amplitude as
 $$\begin{gather} g_{2,1}(t_0) = \frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\gamma_1 \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0, \end{gather}$$
$$\begin{gather} g_{2,1}(t_0) = \frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\gamma_1 \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0, \end{gather}$$ $$\begin{gather}g_{2,2}(t_0) ={-}\frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\gamma_2 \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0 . \end{gather}$$
$$\begin{gather}g_{2,2}(t_0) ={-}\frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\gamma_2 \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0 . \end{gather}$$The time scale of the first wave can be written as
 \begin{align} \left.\begin{gathered}
t_0 = t, \\ \begin{aligned}t_1 &={-}\frac{\omega t_0
(\bar{\zeta} + \sqrt{\bar{\zeta}^2 - 4
{\rm \pi}^2})}{2 {\rm \pi}} \cr
&\quad +\, \frac{K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 -
\bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,
\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\omega
\left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0 +
\cdots,\end{aligned}
\end{gathered}\right\}\end{align}
\begin{align} \left.\begin{gathered}
t_0 = t, \\ \begin{aligned}t_1 &={-}\frac{\omega t_0
(\bar{\zeta} + \sqrt{\bar{\zeta}^2 - 4
{\rm \pi}^2})}{2 {\rm \pi}} \cr
&\quad +\, \frac{K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 -
\bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,
\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\omega
\left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0 +
\cdots,\end{aligned}
\end{gathered}\right\}\end{align}while the time scale of the wave travelling in the opposite direction is
 \begin{equation} \left.\begin{gathered}
t_0 = t, \\ \begin{aligned}t_1 &= \frac{\omega t_0
(-\bar{\zeta} + \sqrt{\bar{\zeta}^2 - 4
{\rm \pi}^2})}{2 {\rm \pi}} \cr
&\quad- \,\frac{K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 -
\bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,
\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\omega
\left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0 +
\cdots. \end{aligned}\end{gathered}\right\}
\end{equation}
\begin{equation} \left.\begin{gathered}
t_0 = t, \\ \begin{aligned}t_1 &= \frac{\omega t_0
(-\bar{\zeta} + \sqrt{\bar{\zeta}^2 - 4
{\rm \pi}^2})}{2 {\rm \pi}} \cr
&\quad- \,\frac{K
{\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 -
\bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,
\varphi(x_{f})\,\varphi'(x_{f}) \right]}{\omega
\left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t_0 +
\cdots. \end{aligned}\end{gathered}\right\}
\end{equation}
The terms ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _2$ have been set to
$\gamma _2$ have been set to ![]() $1$ without loss of generality. Such a time scale analysis can also be performed employing the Wentzel–Kramers–Brillouin (WKB) approach. The derivation of the solutions is demonstrated in Appendix A, showing and thereby verifying that the WKB approach scales align with the generalized scaling approach.
$1$ without loss of generality. Such a time scale analysis can also be performed employing the Wentzel–Kramers–Brillouin (WKB) approach. The derivation of the solutions is demonstrated in Appendix A, showing and thereby verifying that the WKB approach scales align with the generalized scaling approach.
Several conclusions can be drawn from this solution and its respective scales. First, the solution takes the form of hyperbolic cosine and sine waves travelling in opposite directions, resembling the response of a damped oscillator. The heater power influences the amplitude of these waves. Additionally, factors such as time delay and acoustic intensity at the heater location contribute to the amplitude response. For the transient response, the damping primarily controls the fast oscillatory scale, while heat release, delay and acoustic intensity at the heater location influence the slower time scale.
2.3. Method validation
Figure 5 compares the theoretical Rijke tube data with the EVDP equation results. While minor phase lag deviations can be observed during the initial transient, the limit cycle prediction is reasonably accurate. The limit cycle amplitude, frequency, and the time required to reach the limit cycle agree well between the models. The statistical error of the EVDP system and the input system, the limit cycle amplitude and frequency, are chosen as the specific, quantifiable metrics, which are 1.4 % and 1.8 %, respectively, in figure 5.

Figure 5. Comparison of the Rijke tube model and the EVDP model (![]() $\mu _1=0.016$,
$\mu _1=0.016$, ![]() $\mu _2=0.472$,
$\mu _2=0.472$, ![]() $\mu _3=4.515$), for (a) oscillations and (b) frequency.
$\mu _3=4.515$), for (a) oscillations and (b) frequency.
Further validation is conducted on a modelled standing-wave thermoacoustic system with heat exchangers applied (aiming to create temperature gradient across the stack). The modelled systems consist of Navier–Stokes governing equations (PDEs). The modelled standing-wave TAE is three-dimensional. It is a simplified cylindrical tube with the left end rigidly closed (acoustic velocity node) and the right end open (acoustic pressure node). The TAE system is simulated numerically with standing ![]() $k$-
$k$-![]() $\epsilon$ of the WALE-LES turbulence model, and resolved in the computational fluid dynamics (CFD) solver ANSYS Fluent 19.0. More details like boundary conditions, computational settings (turbulence model) and validations can be found in previous work (Guo et al. Reference Guo, Zhao, Xu, Tokhi and Karimi2023). The pressure fluctuations generated from the modelled TAE system are shown in figure 6(a). Before the limit cycle oscillations (LCOs) are generated, the flow disturbances decay rapidly first and then grow gradually. The decay behaviour is due to the initial energy dissipation. (The energy dissipates when pressure oscillation is not in phase with the unsteady heat release perturbations according to the Rayleigh criterion.) Therefore, the perturbations in the red circle (describing the rapid decay process) are neglected and deleted. The rest time series is non-dimensionalized to get the input data (figure 6b). After training the PINNs model,
$\epsilon$ of the WALE-LES turbulence model, and resolved in the computational fluid dynamics (CFD) solver ANSYS Fluent 19.0. More details like boundary conditions, computational settings (turbulence model) and validations can be found in previous work (Guo et al. Reference Guo, Zhao, Xu, Tokhi and Karimi2023). The pressure fluctuations generated from the modelled TAE system are shown in figure 6(a). Before the limit cycle oscillations (LCOs) are generated, the flow disturbances decay rapidly first and then grow gradually. The decay behaviour is due to the initial energy dissipation. (The energy dissipates when pressure oscillation is not in phase with the unsteady heat release perturbations according to the Rayleigh criterion.) Therefore, the perturbations in the red circle (describing the rapid decay process) are neglected and deleted. The rest time series is non-dimensionalized to get the input data (figure 6b). After training the PINNs model, ![]() $\mu _1=0.0303$,
$\mu _1=0.0303$, ![]() $\mu _2=0.00648$ and
$\mu _2=0.00648$ and ![]() $\mu _3=1.72$ are obtained. As shown in figures 6(c) and 6(d), the oscillations predicted from EVDP with variables obtained from PINNs fit well with the CFD model, and the error of the frequency and the limit cycle amplitude are 0.02 % and 0.05 %, respectively.
$\mu _3=1.72$ are obtained. As shown in figures 6(c) and 6(d), the oscillations predicted from EVDP with variables obtained from PINNs fit well with the CFD model, and the error of the frequency and the limit cycle amplitude are 0.02 % and 0.05 %, respectively.

Figure 6. Validation of the PINNs-EVDP model with CFD data: (a) original data; (b) data processing; (c,d) comparison with the EVDP system.
In general, the errors between these two data sets are acceptable. The validations of the two cases consisting of both ODE and PDE modelled thermoacoustic systems provide convincing evidence supporting the effectiveness and correctness of the proposed model to describe the nonlinear system reliably. Further investigations and comparisons can be conducted to examine the bifurcation characteristics of the coupled thermoacoustic systems.
3. Results
To illustrate the proposed model capabilities, the suppression of the hazardous thermoacoustic instability by the coupling method is demonstrated in this section. The amplitude reduction effect is verified in Appendix C based on the coupled simulation model mentioned before. Additionally, previous work (Biwa et al. Reference Biwa, Tozuka and Yazaki2015; Thomas et al. Reference Thomas, Mondal, Pawar and Sujith2018; Ghosh, Mondal & Sujith Reference Ghosh, Mondal and Sujith2022) showed that the governing equations describing the coupled dynamics of the thermoacoustic systems ‘a’ and ‘b’ can be expressed as
 \begin{align}
\frac{{\rm d}\dot{\eta}^a}{{\rm
d}t}+\omega_a^2\eta^a+\zeta\dot{\eta}^a&=
\frac{\beta_a}{E_a}\,\varphi^a(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'_{n}(x_{f})\,\eta^a(t-\tau_1)\right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}\nonumber\\
&\quad
+K_{d}(\dot{\eta}^b-\dot{\eta}^a)+K_{\tau}[\dot{\eta}^b(t-\tau_2)-\dot{\eta}^a(t)]
\end{align}
\begin{align}
\frac{{\rm d}\dot{\eta}^a}{{\rm
d}t}+\omega_a^2\eta^a+\zeta\dot{\eta}^a&=
\frac{\beta_a}{E_a}\,\varphi^a(x_{f})\biggl\{\left|\frac{1}{3}-\varphi'_{n}(x_{f})\,\eta^a(t-\tau_1)\right|^{1/2}-\left(\frac{1}{3}\right)^{1/2}\biggr\}\nonumber\\
&\quad
+K_{d}(\dot{\eta}^b-\dot{\eta}^a)+K_{\tau}[\dot{\eta}^b(t-\tau_2)-\dot{\eta}^a(t)]
\end{align}
for coupled theoretical Rijke tubes, and
for coupled EVDP systems (where the equations for the coupled thermoacoustic system b can be obtained by alternating the superscripts). The coefficients ![]() $K_{d}$ and
$K_{d}$ and ![]() $K_{\tau }$ represent the strength of the dissipative and time-delay coupling effects, respectively, which could be controlled by a needle valve and a vinyl tube (Biwa et al. Reference Biwa, Tozuka and Yazaki2015). The dissipative coupling strength (
$K_{\tau }$ represent the strength of the dissipative and time-delay coupling effects, respectively, which could be controlled by a needle valve and a vinyl tube (Biwa et al. Reference Biwa, Tozuka and Yazaki2015). The dissipative coupling strength (![]() $K_{d}$), detuning (the frequency ratio
$K_{d}$), detuning (the frequency ratio ![]() $R_{\omega }=\omega _1/\omega _2$), time-delay coupling strength (
$R_{\omega }=\omega _1/\omega _2$), time-delay coupling strength (![]() $K_{\tau }$) and time delay (
$K_{\tau }$) and time delay (![]() $\tau _2$) are four control parameters that need to be determined. All ODEs are solved numerically by a fourth-order Runge–Kutta scheme.
$\tau _2$) are four control parameters that need to be determined. All ODEs are solved numerically by a fourth-order Runge–Kutta scheme.
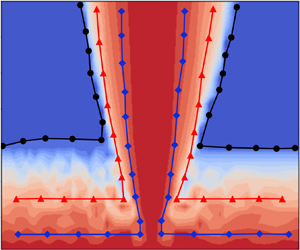
3.1. Effect of time-delay coupling
Due to the time required for a signal to travel from one system to another, the coupling process involves time delays. The time-delay coupling effects are illustrated in figure 7, based on the oscillator located on the right-hand side of the Hopf point (which can be seen in figure 4a) without considering dissipative coupling and detuning. The bifurcation curves shown in figure 7(d), delineating the parameter plane into regions of AD and LCO, exhibit a consistent pattern for both coupled systems at small time delays. The one-parameter bifurcation diagrams plotted in figures 7(a) and 7(c) reveal a small discrepancy in point ![]() $A$ with
$A$ with ![]() $K_\tau =0.2$ and
$K_\tau =0.2$ and ![]() $\tau _2=0.2$. The coupled oscillation is depicted in figure 8(a) and demonstrates a faster decay towards AD in the theoretical, coupled Rijke tube systems compared to the coupled EVDP systems. The oscillation amplitude in the EVDP systems decreases more slowly, but AD will be reached when sufficient simulation time is provided. In conclusion, the coupled systems based on the proposed EVDP approach can accurately predict the time-delay coupling effects when the time delay is smaller than the central point. The central point, identified as the point around which the AD occurs most efficiently, is found to be near
$\tau _2=0.2$. The coupled oscillation is depicted in figure 8(a) and demonstrates a faster decay towards AD in the theoretical, coupled Rijke tube systems compared to the coupled EVDP systems. The oscillation amplitude in the EVDP systems decreases more slowly, but AD will be reached when sufficient simulation time is provided. In conclusion, the coupled systems based on the proposed EVDP approach can accurately predict the time-delay coupling effects when the time delay is smaller than the central point. The central point, identified as the point around which the AD occurs most efficiently, is found to be near ![]() $\omega \tau _2=0.815{\rm \pi}$ in the current study. The central point was found to be
$\omega \tau _2=0.815{\rm \pi}$ in the current study. The central point was found to be ![]() $\omega \tau _2={\rm \pi}$ in Thomas et al. (Reference Thomas, Mondal, Pawar and Sujith2018), and
$\omega \tau _2={\rm \pi}$ in Thomas et al. (Reference Thomas, Mondal, Pawar and Sujith2018), and ![]() $\omega \tau _2={\rm \pi} /2$ in Biwa et al. (Reference Biwa, Tozuka and Yazaki2015). The amplitude reduction may be attributed to the negative feedback resulting from self-sustained oscillations and phase-lagged oscillations of the feedback signal (Thomas et al. Reference Thomas, Mondal, Pawar and Sujith2018).
$\omega \tau _2={\rm \pi} /2$ in Biwa et al. (Reference Biwa, Tozuka and Yazaki2015). The amplitude reduction may be attributed to the negative feedback resulting from self-sustained oscillations and phase-lagged oscillations of the feedback signal (Thomas et al. Reference Thomas, Mondal, Pawar and Sujith2018).

Figure 7. Effects of coupling strength (![]() $K_\tau$) and time delay (
$K_\tau$) and time delay (![]() $\tau _2$) in the coupling Rijke tube system and the EVDP system symbolized by the amplitude of the end cycle. (No dissipative coupling and detuning effects with
$\tau _2$) in the coupling Rijke tube system and the EVDP system symbolized by the amplitude of the end cycle. (No dissipative coupling and detuning effects with ![]() $K_{d}=0$ and
$K_{d}=0$ and ![]() $R_\omega =1$.) One-parameter bifurcation diagrams with (a)
$R_\omega =1$.) One-parameter bifurcation diagrams with (a) ![]() $\tau _2=0.2$, (b)
$\tau _2=0.2$, (b) ![]() $\tau _2=1.1$, (c)
$\tau _2=1.1$, (c) ![]() $K_\tau =0.2$. (d) Two-parameter bifurcation diagram in the parameter plane. The points A, B, C in figure 7(d) are correspondingly plotted in the time domains in figure 8(a), (b) and (c), respectively. Here,
$K_\tau =0.2$. (d) Two-parameter bifurcation diagram in the parameter plane. The points A, B, C in figure 7(d) are correspondingly plotted in the time domains in figure 8(a), (b) and (c), respectively. Here, ![]() $A_{lc}$ represents the amplitude of the limit cycle when it is stabilized.
$A_{lc}$ represents the amplitude of the limit cycle when it is stabilized.

Figure 8. Coupling oscillations of the coupling systems at the following points: (a) ![]() $A$ with
$A$ with ![]() $\tau _2=0.2$ and
$\tau _2=0.2$ and ![]() $K_\tau =0.2$; (b)
$K_\tau =0.2$; (b) ![]() $B$ with
$B$ with ![]() $\tau _2=1.1$ and
$\tau _2=1.1$ and ![]() $K_\tau =0.2$; (c)
$K_\tau =0.2$; (c) ![]() $C$ with
$C$ with ![]() $\tau _2=1.2$ and
$\tau _2=1.2$ and ![]() $K_\tau =0.2$.
$K_\tau =0.2$.
Upon passing the central point, the differences in the predictions become evident. Figure 7(b) shows that the EVDP systems require a smaller time-delay coupling strength to achieve AD at large time delays (![]() $\tau _2>0.7$). At point
$\tau _2>0.7$). At point ![]() $B$ (as shown in figure 8b), the coupled EVDP systems decay to AD, while the theoretical, coupled Rijke tube systems experience a decrease in amplitude before settling into a low-amplitude steady state. This observation suggests that the theoretical and dynamic differences between these two systems are not the same. Comparing (2.2) and (2.22), using the EVDP equation as the alternative system, transfers the nonlinearity from the source term to the damping term, which makes the strong nonlinear system a weaker nonlinear system. Due to this transfer of nonlinearity, the bifurcation difference is unavoidable. Therefore, when time delay
$B$ (as shown in figure 8b), the coupled EVDP systems decay to AD, while the theoretical, coupled Rijke tube systems experience a decrease in amplitude before settling into a low-amplitude steady state. This observation suggests that the theoretical and dynamic differences between these two systems are not the same. Comparing (2.2) and (2.22), using the EVDP equation as the alternative system, transfers the nonlinearity from the source term to the damping term, which makes the strong nonlinear system a weaker nonlinear system. Due to this transfer of nonlinearity, the bifurcation difference is unavoidable. Therefore, when time delay ![]() $\tau _2$, which influences the nonlinearity of the system, is small, the differences of the AD region are small, while when time delay
$\tau _2$, which influences the nonlinearity of the system, is small, the differences of the AD region are small, while when time delay ![]() $\tau _2$ increases, the difference is intensified as shown in figure 7(d). This divergence of AD results in the coupled proposed alternative system exhibiting a slightly wider AD region. Hence the proposed method will be more reliable with a small
$\tau _2$ increases, the difference is intensified as shown in figure 7(d). This divergence of AD results in the coupled proposed alternative system exhibiting a slightly wider AD region. Hence the proposed method will be more reliable with a small ![]() $\tau _2$ value for a controller strategy, when using the alternative EVDP system to determine the coupling parameters.
$\tau _2$ value for a controller strategy, when using the alternative EVDP system to determine the coupling parameters.
3.2. Effect of dissipative coupling
To investigate the impact of dissipative coupling, two non-identical Rijke tubes (with natural frequency ratio ![]() $R_\omega =0.878$) are designed with the theoretical model for coupling by adjusting the temperature gradient across the heat source. The temporal perturbations are then used to learn the proposed EVDP model. Figure 9 shows the model results when weak and strong dissipative coupling effects are applied without time-delay coupling (
$R_\omega =0.878$) are designed with the theoretical model for coupling by adjusting the temperature gradient across the heat source. The temporal perturbations are then used to learn the proposed EVDP model. Figure 9 shows the model results when weak and strong dissipative coupling effects are applied without time-delay coupling (![]() $K_\tau =0$). The coupled EVDP oscillators exhibit almost identical behaviour regardless of the dissipative coupling strength. For low dissipative coupling strength, the oscillators settle into a low-amplitude LCO state. The coupled oscillation amplitudes exhibit periodic variations attributed to the weak interaction effects between the coupled oscillators with close but unequal natural frequencies. The oscillation amplitudes diminish to AD with sufficiently high dissipative coupling strength (
$K_\tau =0$). The coupled EVDP oscillators exhibit almost identical behaviour regardless of the dissipative coupling strength. For low dissipative coupling strength, the oscillators settle into a low-amplitude LCO state. The coupled oscillation amplitudes exhibit periodic variations attributed to the weak interaction effects between the coupled oscillators with close but unequal natural frequencies. The oscillation amplitudes diminish to AD with sufficiently high dissipative coupling strength (![]() $K_{d}=0.18$ in figure 9b).
$K_{d}=0.18$ in figure 9b).

Figure 9. Coupling oscillations when the dissipative coupling is applied: (a) weak dissipative coupling; (b) strong dissipative coupling. For these cases, ![]() $K_\tau =0$ and
$K_\tau =0$ and ![]() $R_\omega =0.878$.
$R_\omega =0.878$.
One-parameter bifurcation plots, shown in figure 10, illustrate the effect of the natural frequency ratios on the oscillation amplitudes. The coupled oscillators exhibit LCO behaviour only when the frequency ratio is close to 1, regardless of the coupling strength. Hence the theoretical Rijke tube and EVDP systems need substantial natural frequency differences to approach AD states. The bifurcation characteristics of these two systems are similar, but the EVDP system predicts wider AD regions.

Figure 10. One-parameter bifurcation diagrams varying the natural frequency ratio, where ![]() $K_\tau =0$: (a)
$K_\tau =0$: (a) ![]() $K_{d}=0.10$, and (b)
$K_{d}=0.10$, and (b) ![]() $K_{d}=0.18$.
$K_{d}=0.18$.
The two-parameter bifurcation diagram for the theoretical, coupled Rijke tube systems is plotted in figure 11(a) to explain the change of the AD region with increasing ![]() $K_{d}$. The blue areas represent the AD phenomenon, i.e. the limit cycle amplitude approaches zero. The system cannot approach AD regardless of the detuning strength until the dissipative strength of the coupling reaches a 0.083 bifurcation value. At this critical point, an important region of AD emerges suddenly. The AD region gradually decreases as the dissipative strength continues increasing beyond this point. This is consistent with the results shown in figure 10. Biwa et al. (Reference Biwa, Tozuka and Yazaki2015) also reported that the oscillation amplitudes controlled by the heater power value (
$K_{d}$. The blue areas represent the AD phenomenon, i.e. the limit cycle amplitude approaches zero. The system cannot approach AD regardless of the detuning strength until the dissipative strength of the coupling reaches a 0.083 bifurcation value. At this critical point, an important region of AD emerges suddenly. The AD region gradually decreases as the dissipative strength continues increasing beyond this point. This is consistent with the results shown in figure 10. Biwa et al. (Reference Biwa, Tozuka and Yazaki2015) also reported that the oscillation amplitudes controlled by the heater power value (![]() $\beta$) impacted the coupling. Hence diagrams with different
$\beta$) impacted the coupling. Hence diagrams with different ![]() $\beta$ values are presented in figure 11(b), showing that higher heater power values require higher dissipative coupling or detuning strength to attain AD. Thus a rising
$\beta$ values are presented in figure 11(b), showing that higher heater power values require higher dissipative coupling or detuning strength to attain AD. Thus a rising ![]() $\beta$ value amplifies the limit cycle amplitude and reduces the AD region.
$\beta$ value amplifies the limit cycle amplitude and reduces the AD region.

Figure 11. Two-parameter bifurcation diagram with varying ![]() $R_\omega$ and
$R_\omega$ and ![]() $K_d$ for the Rijke tube system for (a)
$K_d$ for the Rijke tube system for (a) ![]() $\beta =2.11$, (b)
$\beta =2.11$, (b) ![]() $\beta =4.11$, with the bifurcation curves plotted for different
$\beta =4.11$, with the bifurcation curves plotted for different ![]() $\beta$ values.
$\beta$ values.
The two-parameter bifurcation analysis is also carried out for the coupled EVDP systems. Figure 12(a) reveals that the two-parameter plane is divided into two distinct regions resembling the pattern observed in figure 11. Comparing figures 12(a) and 12(b) (where ![]() $\mu _2$ is decreased and
$\mu _2$ is decreased and ![]() $\mu _1$ is equal) reveals only a minor amplitude decrease with an unchanged bifurcation boundary. Hence
$\mu _1$ is equal) reveals only a minor amplitude decrease with an unchanged bifurcation boundary. Hence ![]() $\mu _2$ damps the oscillation amplitude, and changes of
$\mu _2$ damps the oscillation amplitude, and changes of ![]() $\mu _2$ have negligible effects on the dissipative coupling. However, changing the
$\mu _2$ have negligible effects on the dissipative coupling. However, changing the ![]() $\mu _1$ value causes a distinct behaviour, as shown in figure 12(c) (where
$\mu _1$ value causes a distinct behaviour, as shown in figure 12(c) (where ![]() $\mu _2$ is held constant and
$\mu _2$ is held constant and ![]() $\mu _1$ is increased). Here,
$\mu _1$ is increased). Here, ![]() $\mu _1$ and
$\mu _1$ and ![]() $\beta$ have similar properties, i.e. higher parameter values increase the limit cycle amplitude and extend the LCO region. These observations suggest that the parameter
$\beta$ have similar properties, i.e. higher parameter values increase the limit cycle amplitude and extend the LCO region. These observations suggest that the parameter ![]() $\mu _1$ in the EVDP model mimics the heating power
$\mu _1$ in the EVDP model mimics the heating power ![]() $\beta$ in the theoretical Rijke-type thermoacoustics system. Thus, the EVDP equation can be rearranged such that the ‘source’ term with coefficient
$\beta$ in the theoretical Rijke-type thermoacoustics system. Thus, the EVDP equation can be rearranged such that the ‘source’ term with coefficient ![]() $\mu _1$ is on the right-hand side of the equation:
$\mu _1$ is on the right-hand side of the equation:

Figure 12. Two-parameter bifurcation diagram illustrating variations in ![]() $R_\omega$ and
$R_\omega$ and ![]() $K_{d}$ for the EVDP system (
$K_{d}$ for the EVDP system (![]() ${\mu _3=4.5}$), for (a)
${\mu _3=4.5}$), for (a) ![]() $\mu _1=0.016$,
$\mu _1=0.016$, ![]() $\mu _2=0.5$, (b)
$\mu _2=0.5$, (b) ![]() $\mu _1=0.016$,
$\mu _1=0.016$, ![]() $\mu _2=0.2$, (c)
$\mu _2=0.2$, (c) ![]() $\mu _1=0.032$,
$\mu _1=0.032$, ![]() $\mu _2=0.5$, with the bifurcation curves plotted for different
$\mu _2=0.5$, with the bifurcation curves plotted for different ![]() $\mu _1$ values.
$\mu _1$ values.
The EVDP equation can be interpreted physically. Based on (2.10), the amplitude of the EVDP system is facilitated by raising ![]() $\mu _1$ and decreasing
$\mu _1$ and decreasing ![]() $\mu _2$, while according to Euler's formula, the real part of the exponent influences the amplitude of the oscillation, and the imaginary part determines the frequency of the function. Therefore, based on the results (2.40) and (2.46) from such a generalized scaling method, the amplitude of
$\mu _2$, while according to Euler's formula, the real part of the exponent influences the amplitude of the oscillation, and the imaginary part determines the frequency of the function. Therefore, based on the results (2.40) and (2.46) from such a generalized scaling method, the amplitude of ![]() $\eta$ is influenced by the heating power (enhancing it) and damping (diminishing it), which is consistent with the results obtained from (2.10) as shown in figure 2. According to the comparison of the two-parameter bifurcation diagram, the variable
$\eta$ is influenced by the heating power (enhancing it) and damping (diminishing it), which is consistent with the results obtained from (2.10) as shown in figure 2. According to the comparison of the two-parameter bifurcation diagram, the variable ![]() $\mu _1$ contributes the same efforts of the heating power to the Rijke tube system, and the variable
$\mu _1$ contributes the same efforts of the heating power to the Rijke tube system, and the variable ![]() $\mu _2$ corresponds to the damping term, which have the same contributions to the amplitude of coupled EVDP systems. More accurately, the rising
$\mu _2$ corresponds to the damping term, which have the same contributions to the amplitude of coupled EVDP systems. More accurately, the rising ![]() $\mu _1$ enhances the oscillations and leads to the same type of AD boundary, while the increasing
$\mu _1$ enhances the oscillations and leads to the same type of AD boundary, while the increasing ![]() $\mu _2$ diminishes the amplitude, which is visually evident from figure 12(a) with figure 12(b). Thus we can draw the physical relevance of these variables and get the one-to-one correspondence between (2.20) and (2.2) from the EVDP system to the Rijke-type thermoacoustic system: the coefficient term
$\mu _2$ diminishes the amplitude, which is visually evident from figure 12(a) with figure 12(b). Thus we can draw the physical relevance of these variables and get the one-to-one correspondence between (2.20) and (2.2) from the EVDP system to the Rijke-type thermoacoustic system: the coefficient term ![]() $\mu _2$ represents the system damping, the coefficient term
$\mu _2$ represents the system damping, the coefficient term ![]() $\mu _3$ integrates the frequency information of the thermoacoustic system, and the coefficient term
$\mu _3$ integrates the frequency information of the thermoacoustic system, and the coefficient term ![]() $\mu _1$ can be regarded as the source term of the system, representing the instability intensity introduced by the nonlinear heat source.
$\mu _1$ can be regarded as the source term of the system, representing the instability intensity introduced by the nonlinear heat source.
As for the oscillations observed from the single TAE system, the coupling bifurcation characteristics for the coupled EVDP systems need to be further validated based on either experimental tests or numerical simulations. As reported in previous work (Biwa et al. Reference Biwa, Tozuka and Yazaki2015), the classical VDP system can reproduce the experimental systems. Therefore, the bifurcation investigation of coupled EVDP systems is conducted and shown in figure 13. As depicted in figure 13, cases 1 and 2 are coupled solely by the dissipative coupling, while cases 3 and 4 involve both the dissipative and time-delay couplings. Additionally, cases 1 and 3 represent the EVDP system (when ![]() $\mu _1=\mu _2$), and cases 2 and 4 represent the EVDP system (when
$\mu _1=\mu _2$), and cases 2 and 4 represent the EVDP system (when ![]() $\mu _1\ne \mu _2$). In other words, the EVDP system has the potential to replicate the experimental thermoacoustic system, although the hydrodynamic equations governing thermoacoustic oscillators are far more complicated. Selecting a proper EVDP system to be the alternative system for the system identification is appropriate for the coupling method as discussed in the present work.
$\mu _1\ne \mu _2$). In other words, the EVDP system has the potential to replicate the experimental thermoacoustic system, although the hydrodynamic equations governing thermoacoustic oscillators are far more complicated. Selecting a proper EVDP system to be the alternative system for the system identification is appropriate for the coupling method as discussed in the present work.

Figure 13. Theoretically predicted bifurcation diagrams from our coupled EVDP oscillators (![]() $\mu _3=4.5$). Regions (I) and (II) denote high-amplitude oscillation and AD, respectively.
$\mu _3=4.5$). Regions (I) and (II) denote high-amplitude oscillation and AD, respectively.
Looking forward, while the EVDP system effectively captures the stable periodic solution oscillation or coupling bifurcation, it lacks the subcritical bifurcation features as observed in the Rijke tube system depicted in figure 4 due to its singular bifurcation point (![]() $\mu _1=0$). Additionally, the conversion of such nonlinearity from the source term to the damping term results in a weakened nonlinearity, leading to non-negligible differences in the AD region for coupled systems. Consequently, there is potential to explore better alternative systems for enhancing the PINNs model to yield the characters above. For instance, based on the PINNs model, one may utilize the classical VDP oscillator with a forcing term, the Rijke tube theoretical model, or incorporate multiple modes; all of which may aid in capturing the subcritical bifurcation characteristics of uncoupled system and the AD characteristics of the coupled system. This exploration could significantly enhance the predictive capabilities and further advance our understanding of such complex nonlinear dynamics related to the large-amplitude thermoacoustic instability.
$\mu _1=0$). Additionally, the conversion of such nonlinearity from the source term to the damping term results in a weakened nonlinearity, leading to non-negligible differences in the AD region for coupled systems. Consequently, there is potential to explore better alternative systems for enhancing the PINNs model to yield the characters above. For instance, based on the PINNs model, one may utilize the classical VDP oscillator with a forcing term, the Rijke tube theoretical model, or incorporate multiple modes; all of which may aid in capturing the subcritical bifurcation characteristics of uncoupled system and the AD characteristics of the coupled system. This exploration could significantly enhance the predictive capabilities and further advance our understanding of such complex nonlinear dynamics related to the large-amplitude thermoacoustic instability.
4. Discussion and conclusions
We proposed an approach to find descriptions of the instability behaviour of thermoacoustic systems by exact PDEs, which can be utilized for control strategy analysis. Therefore, the van der Pol (VDP) equation was reformulated, and the unknown parameters were determined using PINNs to solve the inverse problems. The proposed extended VDP (EVDP) model was validated in terms of oscillation and bifurcation characteristics against CFD data of a thermoacoustic engine (TAE) system and a horizontal Rijke tube modelled by the Galerkin series with the modified King's law. Further, the system coupling effect was explored, and control parameters were derived for coupled Rijke tube systems and the coupled EVDP systems. The main findings can be summarized as follows.
(1) The reformulated, nonlinear VDP equation with fitted coefficients by the PINN approach was shown to be capable of replicating the thermoacoustic system instability behaviour. The frequency, limit cycle amplitude, and the time required to reach the limit cycle of the Rijke tube system and the CFD simulation TAE system were predicted accurately. The validation provides evidence for the method's ability to obtain reliable alternative deterministic system descriptions.
(2) The coupled system becomes more prone to AD near a central point with varying time-delay coupling strength. The coupled EVDP systems exhibit almost identical bifurcation characteristics to the coupled Rijke tube system for short time delays on the left-hand side of the central point. For larger time delays, the nonlinear differences between the two systems are amplified, leading to a wider region of AD for the coupled EVDP systems. The differences are unavoidable due to the nonlinearity shift from the source term to the damping term when the EVDP system is used as the alternative system.
(3) The coupled EVDP systems and the coupled Rijke tube systems can attain AD, when the dissipative coupling strength reaches sufficiently high levels or when the natural frequency differences between the coupled systems are significant. As the coupling strength increases, the AD region emerges at specific bifurcation values and diminishes subsequently.
(4) The variable
 $\mu _1$ was shown to affect the two-parameter bifurcation character similarly as the heater power parameter
$\mu _1$ was shown to affect the two-parameter bifurcation character similarly as the heater power parameter  $\beta$, which supports assigning the EVDP model physical significance. The terms with coefficients
$\beta$, which supports assigning the EVDP model physical significance. The terms with coefficients  $\mu _1$,
$\mu _1$,  $\mu _2$ and
$\mu _2$ and  $\mu _3$ can be interpreted as source term, damping term, and term containing the frequency information, respectively.
$\mu _3$ can be interpreted as source term, damping term, and term containing the frequency information, respectively.
Acknowledgements
The authors appreciate the reviewers and the editor for their careful reading and many constructive comments and suggestions on improving the manuscript. The first author would like to acknowledge that the present research was conducted under the supervision of Professor D. Zhao during her CSC-sponsored visit to University of Canterbury in 2023. Dr L. Guo conducted CFD simulations on coupled TAE (standing-wave thermoacoustic engines) systems
Funding
The first author is grateful for the financial support from the Scholarship Council (grant no. 202206130055) for providing scholarship to enable the author to study at the University of Canterbury. This research work is jointly sponsored by the University of Canterbury (grant no.452DISDZ), the National Natural Science Foundation of China (no. 51876056) and Hunan Provincial Innovation Foundation for Postgraduate (no. CX20200413). X.Z. and D.Z. would like to thank the Faculty of Engineering for their financial and computing support.
Declaration of interests
The authors report no conflict of interest.
Author contributions
M.X. wrote the original draft. M.X. processed and analysed the research results and discussed with D.Z., X.Z. and C.S., D.Z. conceived and initialized the project. All authors contributed to the paper writing and English editing. All authors have contributed to the manuscript.
Appendix A. The WKB approach
In order to verify the results from the generalized scaling method, the WKB approximation is carried out. First, the solution ![]() $\eta$ is assumed to have the exponential form
$\eta$ is assumed to have the exponential form
The derivatives may be derived easily as
and
Inserting these expressions into (2.24), a series of three ordinary equations may be derived. The first equation, corresponding to the fast variations in the wave propagation, is the eikonal equation, which is very similar to the equation derived in the generalized scaling method. The next equation is the transport equation, controlling mainly the amplitude of oscillations. Finally, the slow scale ![]() $S_2$ may be resolved. Mathematically, these equations may be written as
$S_2$ may be resolved. Mathematically, these equations may be written as
with
and
For the purposes of verifying the generalized scaling method, initial conditions will not be applied in order to compare the results. First, (A4) may be solved, which is both nonlinear and quadratic with respect to the scale ![]() $S_0$. This matches the same physical explanation given in the generalized scaling method where two waves are moving in opposite directions. The solution may be written as
$S_0$. This matches the same physical explanation given in the generalized scaling method where two waves are moving in opposite directions. The solution may be written as
which reveals the same scales achieved earlier, ![]() $S_0 = g_0$. Next, (A5) is solved for
$S_0 = g_0$. Next, (A5) is solved for ![]() $S_1$ and may be described as
$S_1$ and may be described as
 \begin{equation}
\left.\begin{gathered}
S_{1,1} ={-}\frac{1}{2}\,K t
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr)
\tau_1\,\varphi(x_{f})\,\varphi'(x_{f}),\\
S_{1,2} = \frac{1}{2}\,K t
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f}),
\end{gathered}\right\}
\end{equation}
\begin{equation}
\left.\begin{gathered}
S_{1,1} ={-}\frac{1}{2}\,K t
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} +
1\biggr)
\tau_1\,\varphi(x_{f})\,\varphi'(x_{f}),\\
S_{1,2} = \frac{1}{2}\,K t
\biggl(\frac{\bar{\zeta}}{\sqrt{\bar{\zeta}^2 - 4 {\rm \pi}^2}} -
1\biggr) \tau_1\,\varphi(x_{f})\,\varphi'(x_{f}),
\end{gathered}\right\}
\end{equation}
which corresponds to the exponential argument presented in (2.40). Finally, the scale ![]() $S_2$ may be written as
$S_2$ may be written as
 \begin{equation} \left.\begin{gathered} S_{2,1} = \frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\, \varphi'(x_{f}) \right]}{ \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t,\\ S_{2,2} ={-}\frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f}) \right]}{ \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} S_{2,1} = \frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\, \varphi'(x_{f}) \right]}{ \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t,\\ S_{2,2} ={-}\frac{K {\rm \pi}\,\varphi(x_{f})\,\varphi'(x_{f}) \left[4 {\rm \pi}^2 - \bar{\zeta}^2 + K {\rm \pi}^2 \tau_1^2\,\varphi(x_{f})\,\varphi'(x_{f}) \right]}{ \left(\bar{\zeta}^2 - 4 {\rm \pi}^2\right)^{3/2}}\,t, \end{gathered}\right\} \end{equation}
which is equal to (2.45), i.e. ![]() $S_2 = g_2$. In conclusion, the WKB approach scales align with the generalized scaling approach.
$S_2 = g_2$. In conclusion, the WKB approach scales align with the generalized scaling approach.
Appendix B. Parameters and corresponding values for the modelled system
The critical parameters used in the modelled Rijke tube system in figure 5 in § 2.3 are summarized in table 1.
Table 1. Critical parameters of the dimensionless variable for the modelled Rijke tube system.

Appendix C. Verification of the amplitude suppression effect on the coupling method based on the CFD simulation model
Two numerically modelled TAE systems are coupled by a connecting tube in our CFD simulations, as shown in figure 14. This is an effective coupling method as validated in previous experiments (Hyodo & Biwa Reference Hyodo and Biwa2019). The numerically predicted amplitude reduction from the modelled TAE systems is observed when ![]() $L=800$ mm,
$L=800$ mm, ![]() $d=80$ mm, as depicted in figure 15. The pressure perturbations are attenuated from LCOs with amplitude 5800 Pa to oscillations with maximum amplitude 2900 Pa via a beating behaviour. Correspondingly, the pressure spectra as shown in the frequency domain reveal that the perturbations with a single dominant frequency at 103.7 Hz are changed to those with two dominant frequencies at 95.9 Hz and 105.0 Hz, with a much lower amplitude. All this confirms that the amplitude reduction could be achieved in the modelled coupled TAE systems.
$d=80$ mm, as depicted in figure 15. The pressure perturbations are attenuated from LCOs with amplitude 5800 Pa to oscillations with maximum amplitude 2900 Pa via a beating behaviour. Correspondingly, the pressure spectra as shown in the frequency domain reveal that the perturbations with a single dominant frequency at 103.7 Hz are changed to those with two dominant frequencies at 95.9 Hz and 105.0 Hz, with a much lower amplitude. All this confirms that the amplitude reduction could be achieved in the modelled coupled TAE systems.

Figure 14. Numerically modelled coupled TAE (standing-wave thermoacoustic engines) systems based on previous experiments (Hyodo & Biwa Reference Hyodo and Biwa2019) in the presence of a connecting tube. Here, ![]() $L_A=860\ \textrm {mm}$,
$L_A=860\ \textrm {mm}$, ![]() $L_B=920\ \textrm {mm}$,
$L_B=920\ \textrm {mm}$, ![]() $T_c=300\ \textrm {K}$,
$T_c=300\ \textrm {K}$, ![]() $T_h=425\ \textrm {K}$,
$T_h=425\ \textrm {K}$, ![]() $L=800\ \textrm {mm}$,
$L=800\ \textrm {mm}$, ![]() $d=80\ \textrm {mm}$.
$d=80\ \textrm {mm}$.

Figure 15. Our CFD simulation results of amplitude reduction for the coupled TAE systems via the connecting tube: (a) time evolution of pressure before and after coupling; (b) pressure spectra before coupling; (c) pressure spectra after coupling at ![]() $t=2.45\ \textrm {s}$.
$t=2.45\ \textrm {s}$.