Article contents
Power-law exponent in the transition period of decay in grid turbulence
Published online by Cambridge University Press: 18 August 2015
Abstract
Hot-wire measurements are carried out in grid-generated turbulence at moderate to low Taylor microscale Reynolds number 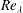 $Re_{{\it\lambda}}$ to assess the appropriateness of the commonly used power-law decay for the mean turbulent kinetic energy (e.g.
$Re_{{\it\lambda}}$ to assess the appropriateness of the commonly used power-law decay for the mean turbulent kinetic energy (e.g. 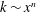 $k\sim x^{n}$ , with
$k\sim x^{n}$ , with 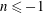 $n\leqslant -1$ ). It is found that in the region outside the initial and final periods of decay, which we designate a transition region, a power law with a constant exponent
$n\leqslant -1$ ). It is found that in the region outside the initial and final periods of decay, which we designate a transition region, a power law with a constant exponent  $n$ cannot describe adequately the decay of turbulence from its initial to final stages. One is forced to use a family of power laws of the form
$n$ cannot describe adequately the decay of turbulence from its initial to final stages. One is forced to use a family of power laws of the form 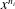 $x^{n_{i}}$ , where
$x^{n_{i}}$ , where 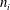 $n_{i}$ is a different constant over a portion
$n_{i}$ is a different constant over a portion 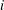 $i$ of the decay time during the decay period. Accordingly, it is currently not possible to determine whether any grid-generated turbulence reported in the literature decays according to Saffman or Batchelor because the reported data fall in the transition period where
$i$ of the decay time during the decay period. Accordingly, it is currently not possible to determine whether any grid-generated turbulence reported in the literature decays according to Saffman or Batchelor because the reported data fall in the transition period where  $n$ differs from its initial and final values. It is suggested that a power law of the form
$n$ differs from its initial and final values. It is suggested that a power law of the form 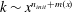 $k\sim x^{n_{init}+m(x)}$ , where
$k\sim x^{n_{init}+m(x)}$ , where 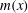 $m(x)$ is a continuous function of
$m(x)$ is a continuous function of  $x$ , could be used to describe the decay from the initial period to the final stage. The present results, which corroborate the numerical simulations of decaying homogeneous isotropic turbulence of Orlandi & Antonia (J. Turbul., vol. 5, 2004, doi:10.1088/1468-5248/5/1/009) and Meldi & Sagaut (J. Turbul., vol. 14, 2013, pp. 24–53), show that the values of
$x$ , could be used to describe the decay from the initial period to the final stage. The present results, which corroborate the numerical simulations of decaying homogeneous isotropic turbulence of Orlandi & Antonia (J. Turbul., vol. 5, 2004, doi:10.1088/1468-5248/5/1/009) and Meldi & Sagaut (J. Turbul., vol. 14, 2013, pp. 24–53), show that the values of  $n$ reported in the literature, and which fall in the transition region, have been mistakenly assigned to the initial stage of decay.
$n$ reported in the literature, and which fall in the transition region, have been mistakenly assigned to the initial stage of decay.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 30
- Cited by


