Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Herbert, Corentin
Pouquet, Annick
and
Marino, Raffaele
2014.
Restricted equilibrium and the energy cascade in rotating and stratified flows.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
374.
Waite, Michael L.
2014.
Modeling Atmospheric and Oceanic Flows.
p.
159.
Waite, Michael L.
and
Snyder, Chris
2014.
Comments on “Indications of Stratified Turbulence in a Mechanistic GCM”.
Journal of the Atmospheric Sciences,
Vol. 71,
Issue. 2,
p.
854.
Gkioulekas, Eleftherios
2014.
Energy and potential enstrophy flux constraints in quasi-geostrophic models.
Physica D: Nonlinear Phenomena,
Vol. 284,
Issue. ,
p.
27.
Kurien, Susan
and
Smith, Leslie M.
2014.
Effect of rotation and domain aspect-ratio on layer formation in strongly stratified Boussinesq flows.
Journal of Turbulence,
Vol. 15,
Issue. 4,
p.
241.
Rosenberg, D.
Pouquet, A.
Marino, R.
and
Mininni, P. D.
2015.
Evidence for Bolgiano-Obukhov scaling in rotating stratified turbulence using high-resolution direct numerical simulations.
Physics of Fluids,
Vol. 27,
Issue. 5,
Xiang, X.
Madison, T. J.
Sellappan, P.
and
Spedding, G. R.
2015.
The turbulent wake of a towed grid in a stratified fluid.
Journal of Fluid Mechanics,
Vol. 775,
Issue. ,
p.
149.
Herbert, Corentin
Marino, Raffaele
Rosenberg, Duane
and
Pouquet, Annick
2016.
Waves and vortices in the inverse cascade regime of stratified turbulence with or without rotation.
Journal of Fluid Mechanics,
Vol. 806,
Issue. ,
p.
165.
Zhai, X. M.
and
Kurien, Susan
2018.
Characteristic length scales of strongly rotating Boussinesq flow in variable-aspect-ratio domains.
Journal of Fluid Mechanics,
Vol. 856,
Issue. ,
p.
397.
Legaspi, Jesse D.
and
Waite, Michael L.
2020.
Prandtl number dependence of stratified turbulence.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Sujovolsky, N. E.
and
Mininni, P. D.
2020.
From waves to convection and back again: The phase space of stably stratified turbulence.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Rosenberg, Duane
Pouquet, Annick
and
Marino, Raffaele
2021.
Correlation between Buoyancy Flux, Dissipation and Potential Vorticity in Rotating Stratified Turbulence.
Atmosphere,
Vol. 12,
Issue. 2,
p.
157.
Koval, A. V.
Gavrilov, N. M.
Kandieva, K. K.
Ermakova, T. S.
and
Didenko, K. A.
2022.
Numerical simulation of stratospheric QBO impact on the planetary waves up to the thermosphere.
Scientific Reports,
Vol. 12,
Issue. 1,
Waite, Michael L.
and
Richardson, Nicholas
2023.
Potential Vorticity Generation in Breaking Gravity Waves.
Atmosphere,
Vol. 14,
Issue. 5,
p.
881.
Labarre, Vincent
Augier, Pierre
Krstulovic, Giorgio
and
Nazarenko, Sergey
2024.
Internal gravity waves in stratified flows with and without vortical modes.
Physical Review Fluids,
Vol. 9,
Issue. 2,
Salhi, A.
Khlifi, A.
Marino, R.
Feraco, F.
Foldes, R.
and
Cambon, C.
2024.
Waves and non-propagating modes in stratified MHD turbulence subject to a weak mean magnetic field.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
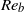 $R{e}_{b} $ ) both smaller and larger than unity. We investigate the conditions under which the potential enstrophy, which is a quartic quantity in the flow variables, can be approximated by its quadratic terms, as is often done in geophysical fluid dynamics. We show that at large scales, the quadratic fraction of the potential enstrophy is determined by
$R{e}_{b} $ ) both smaller and larger than unity. We investigate the conditions under which the potential enstrophy, which is a quartic quantity in the flow variables, can be approximated by its quadratic terms, as is often done in geophysical fluid dynamics. We show that at large scales, the quadratic fraction of the potential enstrophy is determined by 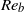 $R{e}_{b} $ . The quadratic part dominates for small
$R{e}_{b} $ . The quadratic part dominates for small 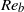 $R{e}_{b} $ , i.e. in the viscously coupled regime of stratified turbulence, but not when
$R{e}_{b} $ , i.e. in the viscously coupled regime of stratified turbulence, but not when  $R{e}_{b} \gtrsim 1$ . The breakdown of the quadratic approximation is consistent with the development of Kelvin–Helmholtz instabilities, which are frequently observed to grow on the layerwise structure of stratified turbulence when
$R{e}_{b} \gtrsim 1$ . The breakdown of the quadratic approximation is consistent with the development of Kelvin–Helmholtz instabilities, which are frequently observed to grow on the layerwise structure of stratified turbulence when 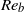 $R{e}_{b} $ is not too small.
$R{e}_{b} $ is not too small.
