Article contents
Playing pool on the beta-plane: how weak initial perturbations predetermine the long-term evolution of coherent vortices
Published online by Cambridge University Press: 22 March 2021
Abstract
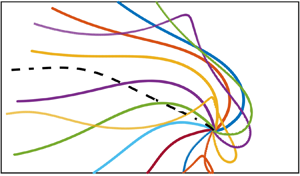
This study explores the long-term impact of a weak initial departure from circular symmetry in coherent equivalent-barotropic vortices on their dynamics and evolution. An algorithm is developed which makes it possible to construct models of vortices that initially propagate with prescribed velocity. These solutions are used as the initial conditions for a series of numerical simulations. Simulations indicate that seemingly minor perturbations of dipolar form can control the propagation of vortices for extended periods, during which they translate over distances greatly exceeding their size. The numerical results are contrasted with the linear model, which assumes that the non-axisymmetric component of circulation in the vortex interior is relatively weak. The linear solutions reflect the self-propagation tendencies of coherent vortices to a much lesser degree, which underscores the role of fundamentally nonlinear mechanisms at play. The remarkable ability of quasi-monopolar vortices to retain the memory of weak initial perturbations helps to rationalize the wide range of the observed propagation velocities of coherent long-lived vortices in the ocean.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by


