Article contents
Phoretic motion in active matter
Published online by Cambridge University Press: 05 July 2021
Abstract
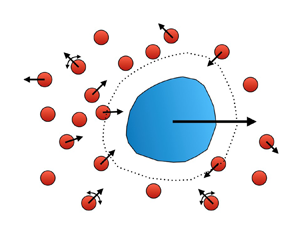
A new continuum perspective for phoretic motion is developed that is applicable to particles of any shape in ‘microstructured’ fluids such as a suspension of solute or bath particles. Using the reciprocal theorem for Stokes flow it is shown that the local osmotic pressure of the solute adjacent to the phoretic particle generates a thrust force (via a ‘slip’ velocity) which is balanced by the hydrodynamic drag such that there is no net force on the body. For a suspension of passive Brownian bath particles this perspective recovers the classical result for the phoretic velocity owing to an imposed concentration gradient. In a bath of active particles that self-propel with characteristic speed  $U_0$ for a time
$U_0$ for a time  $\tau _R$ and then change direction randomly, taking a step of size
$\tau _R$ and then change direction randomly, taking a step of size  $\ell = U_0 \tau _R$, at high activity the phoretic velocity is
$\ell = U_0 \tau _R$, at high activity the phoretic velocity is  $\boldsymbol {U} \sim - U_0 \ell \boldsymbol {\nabla } \phi _b$, where
$\boldsymbol {U} \sim - U_0 \ell \boldsymbol {\nabla } \phi _b$, where  $\phi _b$ is a measure of the ‘volume’ fraction of the active bath particles. The phoretic velocity is independent of the size of the phoretic particle and of the viscosity of the suspending fluid. Because active systems are inherently out of equilibrium, phoretic motion can occur even without an imposed concentration gradient. It is shown that at high activity when the run length varies spatially, net phoretic motion results in
$\phi _b$ is a measure of the ‘volume’ fraction of the active bath particles. The phoretic velocity is independent of the size of the phoretic particle and of the viscosity of the suspending fluid. Because active systems are inherently out of equilibrium, phoretic motion can occur even without an imposed concentration gradient. It is shown that at high activity when the run length varies spatially, net phoretic motion results in  $\boldsymbol {U} \sim - \phi _b U_0 \boldsymbol {\nabla } \ell$. These two behaviours are special cases of the more general result that phoretic motion arises from a gradient in the swim pressure of active matter. Finally, it is shown that a field that orients (but does not propel) the active particles results in a phoretic velocity
$\boldsymbol {U} \sim - \phi _b U_0 \boldsymbol {\nabla } \ell$. These two behaviours are special cases of the more general result that phoretic motion arises from a gradient in the swim pressure of active matter. Finally, it is shown that a field that orients (but does not propel) the active particles results in a phoretic velocity  $\boldsymbol {U} \sim - \phi _b U_0 \ell \boldsymbol {\nabla }\varPsi$, where
$\boldsymbol {U} \sim - \phi _b U_0 \ell \boldsymbol {\nabla }\varPsi$, where  $\varPsi$ is the (non-dimensional) potential associated with the field.
$\varPsi$ is the (non-dimensional) potential associated with the field.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 8
- Cited by


