Article contents
Passive hovering of a flexible 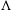 $\unicode[STIX]{x039B}$-flyer in a vertically oscillating airflow
$\unicode[STIX]{x039B}$-flyer in a vertically oscillating airflow
Published online by Cambridge University Press: 04 September 2019
Abstract
We numerically investigate the passive flight of a flexible 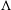 $\unicode[STIX]{x039B}$-flyer in a vertically oscillating airflow with zero mean stream. The flexibility of the flyer is introduced by a torsion spring installed at the hinged joint. We study the effects of spring stiffness, density, resting angle and actuation efforts on the hovering performance. The results suggest that the occurrence of resonance in flexible flyers can result in significantly different performances in flexible and rigid flyers. It is found that flexibility can have two opposing effects, reducing or increasing the actuation efforts for hovering, depending on the range of driving frequency. This result is explained by the modulation of relative motion between the flyer and the imposed background flow due to the involvement of passive angular oscillation. The angular oscillation patterns, the wake symmetry properties and the postural stability behaviours under different driving conditions are also explored. Based on the findings of the present study, the ideal parameter values for stable hovering are suggested. The results of this study offer novel insight into the mechanism by which the flexibility of the flyer affects the passive hovering performance.
$\unicode[STIX]{x039B}$-flyer in a vertically oscillating airflow with zero mean stream. The flexibility of the flyer is introduced by a torsion spring installed at the hinged joint. We study the effects of spring stiffness, density, resting angle and actuation efforts on the hovering performance. The results suggest that the occurrence of resonance in flexible flyers can result in significantly different performances in flexible and rigid flyers. It is found that flexibility can have two opposing effects, reducing or increasing the actuation efforts for hovering, depending on the range of driving frequency. This result is explained by the modulation of relative motion between the flyer and the imposed background flow due to the involvement of passive angular oscillation. The angular oscillation patterns, the wake symmetry properties and the postural stability behaviours under different driving conditions are also explored. Based on the findings of the present study, the ideal parameter values for stable hovering are suggested. The results of this study offer novel insight into the mechanism by which the flexibility of the flyer affects the passive hovering performance.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 6
- Cited by

