Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Ao
Song, Qiang
Ji, Bingqiang
and
Yao, Qiang
2015.
Thermophoretic motion behavior of submicron particles in boundary-layer-separation flow around a droplet.
Physical Review E,
Vol. 92,
Issue. 6,
Espinosa-Gayosso, Alexis
Ghisalberti, Marco
Ivey, Gregory N.
and
Jones, Nicole L.
2015.
Density-ratio effects on the capture of suspended particles in aquatic systems.
Journal of Fluid Mechanics,
Vol. 783,
Issue. ,
p.
191.
Krick, Julian
and
Ackerman, Josef Daniel
2015.
Adding ecology to particle capture models: Numerical simulations of capture on a moving cylinder in crossflow.
Journal of Theoretical Biology,
Vol. 368,
Issue. ,
p.
13.
Wang, Ao
Song, Qiang
and
Yao, Qiang
2016.
Study on inertial capture of particles by a droplet in a wide Reynolds number range.
Journal of Aerosol Science,
Vol. 93,
Issue. ,
p.
1.
Wang, Ao
Song, Qiang
Ji, Bingqiang
and
Yao, Qiang
2017.
In-situ observation of hydrophobic micron particle impaction on liquid surface.
Powder Technology,
Vol. 311,
Issue. ,
p.
408.
McCombe, Dori
and
Ackerman, Josef D.
2018.
Collector Motion Affects Particle Capture in Physical Models and in Wind Pollination.
The American Naturalist,
Vol. 192,
Issue. 1,
p.
81.
Chen, Hongsheng
Liu, Wenwei
and
Li, Shuiqing
2019.
Deposition of wet microparticles on a fiber: Effects of impact velocity and initial spin.
Powder Technology,
Vol. 357,
Issue. ,
p.
83.
Chang, You-Im
Liao, Keng-Yi
and
Jang, Larry
2019.
New correlations for the initial collection efficiency of Brownian aerosol particles with the bounce-off effect considered in granular filtration.
Separation and Purification Technology,
Vol. 229,
Issue. ,
p.
115586.
Irvine, Joshua Lelemia
and
Kim, Albert S.
2019.
Hydraulic design perspectives of bioswale vegetation layers: a meta-research theory.
Desalination and Water Treatment,
Vol. 143,
Issue. ,
p.
137.
Boudina, Mouad
Gosselin, Frédérick P.
and
Étienne, Stéphane
2020.
Direct interception or inertial impaction? A theoretical derivation of the efficiency power law for a simple and practical definition of capture modes.
Physics of Fluids,
Vol. 32,
Issue. 12,
Wang, Ai
Hoque, Mohammad Mainul
Moreno-Atanasio, Roberto
Doroodchi, Elham
Evans, Geoffrey
and
Mitra, Subhasish
2021.
Effect of bubble surface loading on bubble rise velocity.
Minerals Engineering,
Vol. 174,
Issue. ,
p.
107252.
Boudina, Mouad
Gosselin, Frédérick P.
and
Étienne, Stéphane
2021.
Vortex-induced vibrations: a soft coral feeding strategy?.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Shi, Wei
Peruzzo, Paolo
and
Defina, Andrea
2021.
An Eulerian Model for the Transport and Diffusion of Floating Particles Within Regions of Emergent Vegetation.
Water Resources Research,
Vol. 57,
Issue. 8,
Derksen, Jos J.
2021.
Bending and low‐frequency vortex shedding of flexible cylinders in laminar shear flow.
AIChE Journal,
Vol. 67,
Issue. 9,
Espinosa-Gayosso, Alexis
Ghisalberti, Marco
Shimeta, Jeff
Ivey, Gregory N.
and
Tian, Fang-Bao
2021.
On predicting particle capture rates in aquatic ecosystems.
PLOS ONE,
Vol. 16,
Issue. 12,
p.
e0261400.
Shi, Wei
Peruzzo, Paolo
and
Defina, Andrea
2022.
Transient Retention of Floating Particles Captured by Emergent Vegetation Through Capillarity.
Water Resources Research,
Vol. 58,
Issue. 6,
Yu, Congrong
Sun, Xiaolu
Sun, Yufeng
Yang, Kang
and
Yu, Zhongbo
2022.
Colloid‐Pollutant Migration through Saturated Vegetative Filter Strips with Various Hydrodynamics Condition under Rainfall.
JAWRA Journal of the American Water Resources Association,
Vol. 58,
Issue. 6,
p.
1255.
Li, Min
Liu, Haihu
Zhang, Yang
Jia, Pan
Feng, Peihua
and
Yang, Bin
2022.
Two-dimensional characterization of particle entrainment over a downstream obstacle.
International Journal of Multiphase Flow,
Vol. 156,
Issue. ,
p.
104228.
Abolpour, Bahador
Hekmatkhah, Ramtin
and
Shamsoddini, Rahim
2022.
Multi-Objective Optimization of the Particle Trapping Enhancement by Genetic Algorithm and Image Processing Method.
SSRN Electronic Journal ,
Sewak, Kyle
Hassan, Marwan
and
Ackerman, Josef D.
2024.
Fluid-structure interaction of flexible collectors affects particle capture efficiency at ecologically relevant collector Reynolds numbers.
Frontiers in Mechanical Engineering,
Vol. 10,
Issue. ,
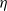 $\eta $ ) of low-inertia particles by a circular cylindrical collector at intermediate Reynolds numbers in the vortex-shedding regime (i.e. for
$\eta $ ) of low-inertia particles by a circular cylindrical collector at intermediate Reynolds numbers in the vortex-shedding regime (i.e. for 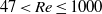 $47\lt \mathit{Re}\leq 1000$ , where
$47\lt \mathit{Re}\leq 1000$ , where 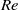 $\mathit{Re}$ is the collector Reynolds number). We demonstrate that vortex shedding induces oscillations near the leading face of the collector which greatly affect the quantity and distribution of captured particles. Unlike in steady, low-
$\mathit{Re}$ is the collector Reynolds number). We demonstrate that vortex shedding induces oscillations near the leading face of the collector which greatly affect the quantity and distribution of captured particles. Unlike in steady, low- 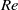 $\mathit{Re}$ flow, particles directly upstream of the collector are not the most likely to be captured. Our results demonstrate the dependence of the time-averaged capture efficiency on
$\mathit{Re}$ flow, particles directly upstream of the collector are not the most likely to be captured. Our results demonstrate the dependence of the time-averaged capture efficiency on 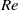 $\mathit{Re}$ and particle size, improving the predictive capability for the capture of particles by aquatic collectors. The transition to theoretical high-Reynolds-number behaviour (i.e.
$\mathit{Re}$ and particle size, improving the predictive capability for the capture of particles by aquatic collectors. The transition to theoretical high-Reynolds-number behaviour (i.e. 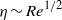 $\eta \sim {\mathit{Re}}^{1/ 2} $ ) is complex due to comparatively rapid changes in wake conditions in this Reynolds number range.
$\eta \sim {\mathit{Re}}^{1/ 2} $ ) is complex due to comparatively rapid changes in wake conditions in this Reynolds number range.
