Article contents
Parametrically forced stably stratified cavity flow: complicated nonlinear dynamics near the onset of instability
Published online by Cambridge University Press: 03 June 2019
Abstract
The dynamics of a fluid-filled square cavity with stable thermal stratification subjected to harmonic vertical oscillations is investigated numerically. The nonlinear responses to this parametric excitation are studied over a comprehensive range of forcing frequencies up to two and a half times the buoyancy frequency. The nonlinear results are in general agreement with the Floquet analysis, indicating the presence of nested resonance tongues corresponding to the intrinsic 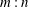 $m:n$ eigenmodes of the stratified cavity. For the lowest-order subharmonic
$m:n$ eigenmodes of the stratified cavity. For the lowest-order subharmonic 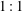 $1:1$ tongue, the responses are analysed in great detail, with complex dynamics identified near onset, most of which involves interactions with unstable saddle states of a homoclinic or heteroclinic nature.
$1:1$ tongue, the responses are analysed in great detail, with complex dynamics identified near onset, most of which involves interactions with unstable saddle states of a homoclinic or heteroclinic nature.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Yalim Supplementary Movie 1
Animation of the vorticity $\eta$ of three limit cycle states corresponding to figure 3 over one response period (two forcing periods). The three limit cycles are L$_{1:2}$ at forcing frequency $\omega=0.91$ with forcing amplitude $\alpha=0.16$, L$_{1:1}$ at $\omega=1.41$ with $\alpha=0.07$, and L$_{2:1}$ at $\omega=1.81$ with $\alpha=0.06$.
Yalim Supplementary Movei 2
Animation corresponding to figure 14, illustrating how the local and global strobe maps of the flow at forcing frequency $\omega=1.35$ vary with forcing amplitude $\alpha$. Demonstrates the homoclinic doubling cascade as $\alpha$ is decreased.
Yalim Supplementary Movie 3
Animation of the isotherms $T$ (first row) and vorticity $\eta$ (second row) of the four indicated limit cycles over two forcing periods at forcing frequency $\omega=1.41$. The limit cycles shown are L$_{1:1}$ at forcing amplitude $\alpha=0.07$ (first column), L$_L$ at $\alpha=0.105$ (second column), L$_R$ at $\alpha=0.105$ (third column), and L$_{2:2}$ at $\alpha=0.105$ (fourth column). Corresponds to figure 15.
Yalim Supplementary Movie 4
Animation of the isotherms $T$ (left column) and vorticity $\eta$ (rightcolumn) for the S$_2$ state at $(\omega,\alpha)=(1.41,0.111)$ over sixforcing periods. Obtained by restricting the direct numerical simulationto the $\Kz$ symmetry subspace. Corresponds to figure 16.
Yalim Supplementary Movie 5
Animation summarizing the dynamics observed in the $\Rpi$ symmetry subspace as an indicated forcing amplitude $\alpha$ is increased by $0.01$ for fixed forcing frequency $\omega=1.41$, with the variance of a horizontal velocity at a point $\varSigma$ (first row, first column), the number of forcing periods $\omega/\omega_R$ associated with the slow response of the 2-tori states (second row, first column), and the associated strobe map sampling a horizontal velocity at a point $u_p$ and a global measure of the temperature $\ET$ every two forcing periods at forcing phase $\pi$ (second column). Corresponds to figure 18.
Yalim Supplementary Movie 6
Animation of the strobe maps of a horizontal velocity at a point with a global measure of the temperature $(u_p,\ET)$ and strobed vorticity $\eta$ of Q$_L$, Q$_R$, and Q at fixed forcing frequency $\omega=1.41$ and indicated forcing amplitude $\alpha$ near the first gluing. Q$_L$ and Q$_R$ are shown at $\alpha=0.125$, and Q is shown at $\alpha=0.126$. The strobe is taken every two forcing periods at forcing phase $\pi$. Corresponds to figure 20.
Yalim Supplementary Movie 7
Animation of the strobe maps of a horizontal velocity at a point with a global measure of the temperature $(u_p,\ET)$ and strobed vorticity $\eta$ of Q$_L$, Q$_R$, and Q at fixed forcing frequency $\omega=1.41$ and indicated forcing amplitude $\alpha$ near the first gluing. Q$_L$ and Q$_R$ are shown at $\alpha=0.125$, and Q is shown at $\alpha=0.126$. The strobe is taken every two forcing periods at forcing phase $\pi$. Corresponds to figure 20.
Yalim Supplementary Movie 8
Animation summarizing the upper-branch dynamics observed in the fullspace as an indicated forcing amplitude $\alpha$ is increased by $0.01$ for fixed forcing frequency $\omega=1.41$, with the variance of a horizontal velocity at a point $\varSigma_u$ (first row, first column), the number of forcing periods $\omega/\omega_R$ associated with the slow response of the 2-tori and 3-tori states (second row, first column), and the associated strobe map sampling a horizontal velocity at a point $u_p$ and a global measure of the temperature $\ET$ every two forcing periods at forcing phase $\pi$ (second column). Corresponds to figure 24.
Yalim Supplementary Movie 9
Animation comparing strobed full space dynamics of Q$_R$ (left column) and T$_{3R}$ (right column) at forcing frequency $\omega=1.41$ and forcing amplitude $\alpha=0.138$ with a two forcing period strobe map of a horizontal velocity at point and a global measure of the temperature $(u_p,\ET)$ at forcing phase $\pi$ (first row) and the strobed vorticity $\eta$ (second row). Corresponds to figure 25.
- 10
- Cited by

