Article contents
Optimal mixing in two-dimensional stratified plane Poiseuille flow at finite Péclet and Richardson numbers
Published online by Cambridge University Press: 23 August 2018
Abstract
We consider the nonlinear optimisation of irreversible mixing induced by an initial finite amplitude perturbation of a statically stable density-stratified fluid with kinematic viscosity  $\unicode[STIX]{x1D708}$ and density diffusivity
$\unicode[STIX]{x1D708}$ and density diffusivity  $\unicode[STIX]{x1D705}$. The initial diffusive error function density distribution varies continuously so that
$\unicode[STIX]{x1D705}$. The initial diffusive error function density distribution varies continuously so that 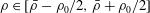 $\unicode[STIX]{x1D70C}\in [\bar{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D70C}_{0}/2,\bar{\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D70C}_{0}/2]$. A constant pressure gradient is imposed in a plane two-dimensional channel of depth
$\unicode[STIX]{x1D70C}\in [\bar{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D70C}_{0}/2,\bar{\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D70C}_{0}/2]$. A constant pressure gradient is imposed in a plane two-dimensional channel of depth 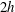 $2h$. We consider flows with a finite Péclet number
$2h$. We consider flows with a finite Péclet number 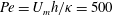 $Pe=U_{m}h/\unicode[STIX]{x1D705}=500$ and Prandtl number
$Pe=U_{m}h/\unicode[STIX]{x1D705}=500$ and Prandtl number 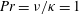 $Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$, and a range of bulk Richardson numbers
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$, and a range of bulk Richardson numbers 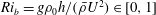 $Ri_{b}=g\unicode[STIX]{x1D70C}_{0}h/(\bar{\unicode[STIX]{x1D70C}}U^{2})\in [0,1]$ where
$Ri_{b}=g\unicode[STIX]{x1D70C}_{0}h/(\bar{\unicode[STIX]{x1D70C}}U^{2})\in [0,1]$ where 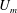 $U_{m}$ is the maximum flow speed of the laminar parallel flow, and
$U_{m}$ is the maximum flow speed of the laminar parallel flow, and 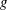 $g$ is the gravitational acceleration. We use the constrained variational direct-adjoint-looping (DAL) method to solve two optimisation problems, extending the optimal mixing results of Foures et al. (J. Fluid Mech., vol. 748, 2014, pp. 241–277) to stratified flows, where the irreversible mixing of the active scalar density leads to a conversion of kinetic energy into potential energy. We identify initial perturbations of fixed finite kinetic energy which maximise the time-averaged perturbation kinetic energy developed over a finite time interval, and initial perturbations that minimise the value (at a target time, chosen to be
$g$ is the gravitational acceleration. We use the constrained variational direct-adjoint-looping (DAL) method to solve two optimisation problems, extending the optimal mixing results of Foures et al. (J. Fluid Mech., vol. 748, 2014, pp. 241–277) to stratified flows, where the irreversible mixing of the active scalar density leads to a conversion of kinetic energy into potential energy. We identify initial perturbations of fixed finite kinetic energy which maximise the time-averaged perturbation kinetic energy developed over a finite time interval, and initial perturbations that minimise the value (at a target time, chosen to be 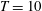 $T=10$) of a ‘mix-norm’ as first introduced by Mathew et al. (Physica D, vol. 211, 2005, pp. 23–46), further discussed by Thiffeault (Nonlinearity, vol. 25, 2012, pp. 1–44) and shown by Foures et al. (2014) to be a computationally efficient and robust proxy for identifying perturbations that minimise the long-time variance of a scalar distribution. We demonstrate, for all bulk Richardson numbers considered, that the time-averaged kinetic-energy maximising perturbations are significantly suboptimal at mixing compared to the mix-norm minimising perturbations, and also that minimising the mix-norm remains (for density-stratified flows) a good proxy for identifying perturbations which minimise the variance at long times. Although increasing stratification reduces the mixing in general, mix-norm minimising optimal perturbations can still trigger substantial mixing for
$T=10$) of a ‘mix-norm’ as first introduced by Mathew et al. (Physica D, vol. 211, 2005, pp. 23–46), further discussed by Thiffeault (Nonlinearity, vol. 25, 2012, pp. 1–44) and shown by Foures et al. (2014) to be a computationally efficient and robust proxy for identifying perturbations that minimise the long-time variance of a scalar distribution. We demonstrate, for all bulk Richardson numbers considered, that the time-averaged kinetic-energy maximising perturbations are significantly suboptimal at mixing compared to the mix-norm minimising perturbations, and also that minimising the mix-norm remains (for density-stratified flows) a good proxy for identifying perturbations which minimise the variance at long times. Although increasing stratification reduces the mixing in general, mix-norm minimising optimal perturbations can still trigger substantial mixing for 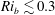 $Ri_{b}\lesssim 0.3$. By considering the time evolution of the kinetic energy and potential energy reservoirs, we find that such perturbations lead to a flow which, through Taylor dispersion, very effectively converts perturbation kinetic energy into ‘available potential energy’, which in turn leads rapidly and irreversibly to thorough and efficient mixing, with little energy returned to the kinetic-energy reservoirs.
$Ri_{b}\lesssim 0.3$. By considering the time evolution of the kinetic energy and potential energy reservoirs, we find that such perturbations lead to a flow which, through Taylor dispersion, very effectively converts perturbation kinetic energy into ‘available potential energy’, which in turn leads rapidly and irreversibly to thorough and efficient mixing, with little energy returned to the kinetic-energy reservoirs.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Marcotte et al. supplementary movie 1
Flow structure at Ri_b=0 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 2
Flow structure at Ri_b=0.05 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 3
Flow structure at Ri_b=0.1 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 4
Flow structure at Ri_b=0.2 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 5
Flow structure at Ri_b=0.5 in the time-integrated-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 6
Flow structure at Ri_b=1 in the time-integrated-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 7
Flow structure at Ri_b=0 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 8
Flow structure at Ri_b=0.05 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 9
Flow structure at Ri_b=0.1 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)
Marcotte et al. supplementary movie 10
Flow structure at Ri_b=0.25 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)
- 15
- Cited by

